1. 시계열 데이터
시계열 데이터란 시간, 순서 정보가 들어 있는 데이터를 말합니다.
문장이 있다면 단어가 나타나는 순서가 중요합니다.
또한 일별 온도를 기록한 데이터가 있다면 날짜의 순서가 중요합니다.
이처럼 데이터에 순서나 시간이 들어가 있는 데이터를 시계열 데이터(time series data)라고 합니다.
시계열 데이터의 독특한 특성에 대해 알아보겠습니다.
- 요소의 순서가 중요
- "세상에는 시계열 데이터가 참 많다"를 "시계열 참 데이터가 많다 세상에는"으로 바꾸면 의미가 훼손됩니다.
- 샘플의 길이가 다름
- 짧은 발음 "인공지능"과 긴 발음 "인 ~공~~~지능"이 다름
- 문맥 의존성
- "시계열은 앞에서 말한 바와 ... 특성이 있다"에서 "시계열은"과 "특성이 있다"는 밀접한 관련성이 있음
- 계절성
- 미세먼지 수치, 항공권 판매량 등
이때 시계열 데이터를 표현하는 방법은 다음과 같습니다.
로 표현됩니다.
이때 t는 시간에 대한 개념입니다. 길이는 가변적이고 벡터의 벡터입니다.
매일 기온, 습도, 미세먼지 농도를 기록한다면
이전에 공부한 SVM, DNN, CNN은 시계열 데이터에 부적합합니다.
왜냐면 위의 모델들은 정적인 데이터를 한꺼번에 입력받아서 처리하기 때문이죠.
즉 샘플의 순서가 전혀 상관이 없습니다. 샘플을 랜덤하게 섞어서 훈련 세트와 검증 세트로 나누기도 했습니다.
심지어 골고루 섞는 편이 더 좋습니다.
하지만 시계열 데이터는 정적 데이터로 변환하여 입력하면 정보의 손실이 매우 큽니다.
또한 시계열 데이터는 샘플의 길이가 다릅니다.
이러한 특성 때문에 시계열 데이터를 인식하는 딥러닝 모델인 RNN과 LSTM이 등장하게 되었습니다.
2. 순환 신경망 (RNN)
대표적인 응용은 미래를 예측하는 것입니다.
또한 언어 번역, 음성 인식 등이 있습니다.
이때 하나의 긴 샘플을 가지고 어떻게 모델링하고 어떻게 미래를 예측하냐?라는 생각이 듭니다.
샘플을 윈도우 크기(w) 단위로 패턴을 잘라 여러 개의 샘플을 수집합니다.
또한 얼마나 먼 미래를 예측할지 지정하는 수평선 계수 (h)가 있습니다.
예를 들어 [12, 10, 8, 15, 16,15]라는 시계열 데이터가 있고, w = 3, h = 1이라고 가정해봅시다.
그렇다면 x는 [12, 10 ,8], [10, 8, 15] , [8, 15, 16] ... 이 되고,
y는 [15, 16, 15]가 됩니다.
y는 label이 되는 셈이죠.
시계열 데이터를 신경망으로 처리하기 위해서는 시간에 따라 값이 하나씩 순차적으로 들어온다는 사실을 반영하는 신경망을 설계해야 합니다.
Input 자체가 순서대로 들어오므로, 이를 신경망에 반영하고, 그 순서를 중요하게 여기면 됩니다.
다행히 DNN을 약간 고쳐서 사용할 수 있습니다.
DNN과 RNN의 차이는
은닉층 노드 사이에 순환 edge가 있다는 사실을 제외하고 동일합니다.
2.1 순환 신경망의 구조
아래의 그림은 RNN의 구조입니다. 먼저 우측을 보시면 됩니다.

보시다시피 RNN은 DNN과 다르게 W라는 가중치 뭉치가 하나 더 필요합니다.
우측 그림을 좌측으로 펼쳐서 보면 이해가 쉽습니다.
h_1에는 단순히 입력 데이터 x_1만 들어갔지만, 첫 번째 노드에서 나온 결과 y_1과 가중치 W가 곱해져서 두 번째 노드에게 전달됩니다.
즉 rnn은 x_i와 이전 타임 스텝의 출력인 y_(i-1)도 함께 받습니다.
이때 타임 스텝에 걸쳐 어떤 상태를 보존하는 신경망의 구성 요소를 메모리 셀 혹은 셀이라고 합니다.
이때 가중치 공유란 순간마다 서로 다른 가중치를 가지는 것이 아니고, 모든 순간이 {U, V, W}를 공유합니다.
왜냐면 RNN은 오른쪽과 같은 형태기 때문에 매 순간마다 다른 가중치를 가질 수 없습니다.
식으로 표현하면 아래와 같습니다.
- i 순간의 x_i는 가중치 U를 통해 은닉층의 상태 h_i에 영향을 미치고, h_i는 가중치 V를 통해 출력값 o_i에 영향을 미침. h_i-1는 가중치 W를 통해 h_i에 영향을 미침
- 은닉층에서 일어나는 계산
- 출력층에서 일어나는 계산
- 은닉층에서의
- RNN은 위의 항을 통해 이전 순간의 은닉층 상태를 현재 순간의 은닉층 상태로 전달하여 시간성을 처리합니다.
RNN에서의 학습은 최적의 {U, V, W}를 알아내는 것이고, BPTT(Back-Propagation Through Time) 알고리즘을 이용하여 알아냅니다.
2.2 순환 신경망의 기억력 한계
이러한 순환 신경망에도 기억력의 한계는 존재합니다.
RNN은 은닉층 상태를 다음 순간으로 넘기는 기능을 통해서 과거를 기억합니다.
하지만 장기 문맥 의존성(멀리 떨어진 요소가 밀접한 상호작용하는 현상)을 제대로 처리하지 못하는 한계를 가지고 있습니다.
예를 들어 (not ~~~~~~~ good) 이런 식으로 되어있다면 분명 좋지 않다는 의미인데, not을 제대로 기억하지 못해서 오히려 좋다고 판단해버리는 경우가 발생할 수 있습니다.
이는 계속 들어오는 input의 영향으로 기억력이 감퇴되는 것입니다.
하지만 사람은 선별적인 기억 능력으로 오래 전 기억을 간직할 수 있죠.
따라서 이러한 선별 기억력을 갖춘 LSTM(long short-term memory) 장단기 메모리 층이 나왔습니다.
3. LSTM (Long Short-Term Memory)
LSTM은 게이트라는 개념으로 선별 기억을 확보합니다.
구조는 아래와 같습니다.

이때 C(Cell state)는 장기 기억 상태이고, H(Hidden State)는 단기 기억 상태라고 볼 수 있습니다.
참고로 입력되는 x나 h, C는 모두 데이터의 벡터로 보셔야 합니다.
- 삭제 게이트(forget gate) (f(t)가 제어함)
- h_(t-1)과 x_(t)가 시그모이드 함수로 들어감
- 이때 시그모이드 함수는 0~1 사이의 값을 출력합니다.
- 만약 0을 출력한다면 기존의 C_(t-1)은 0이 됩니다. 따라서 기억을 완전히 잃어버립니다.
- 하지만 1을 출력한다면 기존의 기억을 유지한 채로 지나갑니다.
- 입력 게이트(input gate) (i(t)가 제어함)
- 현재 입력과 이전 출력으로 만들어진 값, C(t)을 얼마나 cell state에 반영할 것인지를 결정합니다.
- tanh를 통해 어떤 정보를 입력할 건지 후보를 정합니다. tanh는 -1~1까지의 범위로 출력됩니다.
- 이후 시그모이드 함수를 통해서 해당 후보를 얼만큼 cell state에 반영할 것인지 선택합니다.
- 출력 게이트(output gate) (o(t)가 제어함)
- 최종적으로 얻어진 cell state를 tanh 함수에 통과시킵니다.
- 이후 input 된 정보들 역시 시그모이드에 통과시켜 어떤 값을 출력할지 결정합니다.
- 두 값을 곱한 후 최종적인 결괏값을 만듭니다.
- 이에 따라서 결과물은 output으로 나가고, hidden state로 다음 셀에 전달됩니다.
생각보다 많이 복잡하므로 수식은 나중에 쓰도록 하겠습니다.
게이트를 여닫는 정도는 가중치로 표현되며, 이 가중치는 학습으로 알아냅니다.
LSTM에서의 가중치는 RNN에 4개를 추가하여, {U, U_i, U_o, W, W_i, W_o, V}입니다.
이때 i는 입력 게이트, o는 출력 게이트입니다.
간단한 수식으로는 i(t) = sigmoid(x_i * U_i + h_(i-1) * W_i)가 되겠네요.
아무튼 이런 유언한 구조를 가진 LSTM 덕분에 다양한 구조를 설계할 수 있습니다.
3.1 LSTM의 다양한 구조
대표적인 형태가 양방향 LSTM입니다.
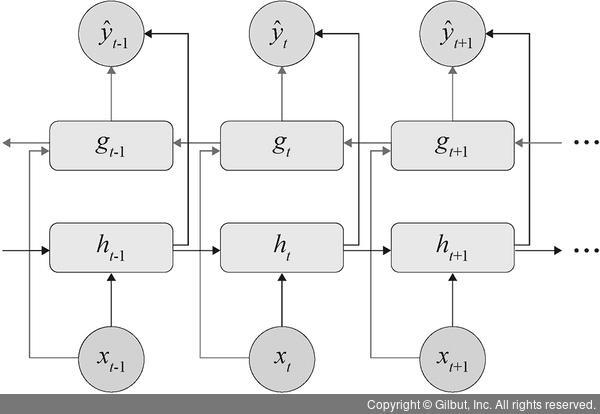
위 그림을 보시면 LSTM이 아래는 우측으로, 위에는 좌측으로 가고 있습니다.
이 방식을 통해 과거에서 미래로 가기도 하고, 미래에서 과거로 가기도 합니다.
또한 이러한 구조도 있습니다.
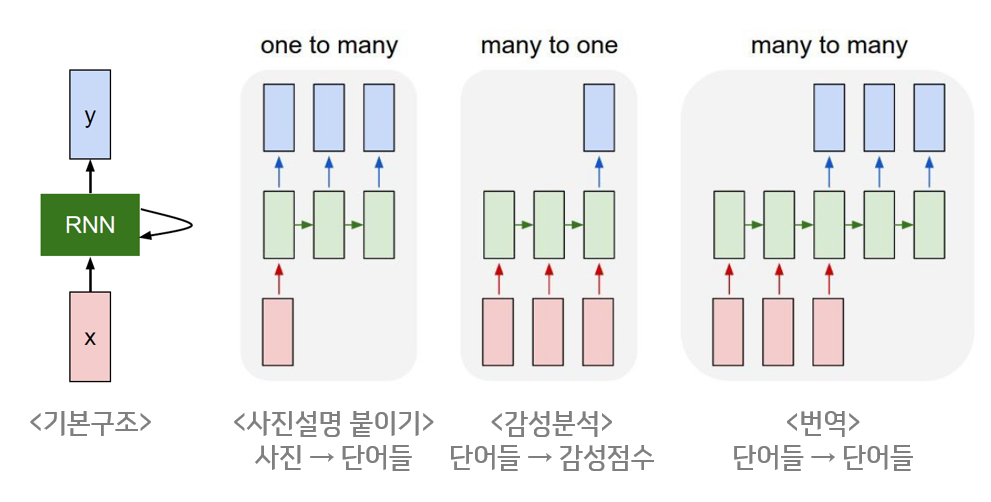
그림으로 보니 이해하기 쉬운 것 같습니다.
4. RNN의 성능 평가
만약 Regression 문제를 푼다면 RNN은 저희가 자주 알던 MAE가 아닌 평균 절댓값 백분율 오차(MAPE)를 이용합니다.
왜냐하면 MAE는 스케일 문제에 대해 대처할 수 없지만, MAPE는 스케일 문제에 대해 대처할 수 있기 때문입니다.
MAPE의 식은 다음과 같습니다.
즉 위 함수를 통해서 평균적으로 얼만큼의 오차가 나는가가 아닌, 평균적으로 얼마만큼의 오차 비율이 나는가? 에 대해 알 수 있습니다.
또 다른 기준으로는 등락 정확률이 있습니다. 이때는 Classifier 문제를 풀 때입니다.
등락 정확률은 등락을 얼마나 정확하게 맞히는지를 측정합니다.
맞힌 경우의 수를 전체 샘플 수로 나눕니다.
| X | Y | Prediction | 맞힘 |
| [..., ..., ..., ..., 21] | 23 | 24 | o |
| [..., ..., ..., ..., 25] | 20 | 26 | x |
| [..., ..., ..., ..., 22] | 24 | 23 | o |
이런 상황이라면 위의 등락 정확률은 2/3이 되겠네요.
5. 요약
시계열 데이터 (Time-Series Data)는 요소의 순서가 중요한 데이터입니다.
RNN은 시계열 데이터를 처리하기 위한 딥러닝 모델입니다.
이때 RNN의 장기 문맥 의존성을 해결하기 위해서 LSTM (long short-term memory)라는 구조가 나왔습니다.
LSTM은 장기 문맥 의존성(장기간 기억하기 위한)을 해결합니다.
어떻게 해결하냐면 선별적 게이트를 통해서 해결합니다.
감사합니다.
지적 환영합니다.