1. CNN의 시작
컴퓨터 비전은 인공지능의 가장 중요한 연구 분야 중 하나입니다.
시각은 인간의 가장 강력한 인지 기능이고, 컴퓨터 비전은 인간의 시각 기능을 모방합니다.
그렇다면 인간의 시각 기능이 어떻게 작동하는지를 먼저 알아야 합니다.
여러분들은 지금 이 글에 집중하고 계실 겁니다.
그러면 옆에 있는 침대, 책상, 책들도 보이실 텐데 흐릿하죠.
결국 시각은 집중하고 있는 field에만 명확히 인식할 수 있습니다.
실제로 시각 피질 안에 많은 뉴런들이 있는데, 어떤 뉴런은 수평선의 이미지에만, 어떤 뉴런은 수직선의 이미지, 또 다른 애는 다른 각도의 선분에만 반응합니다.
또 어떤 뉴런은 큰 수용장을 가져서 더 복잡한 패턴에 반응합니다.
즉 결론적으로 뉴런들은 각기 집중하는 field가 있고, 이 field들이 겹치고 겹쳐서 주위는 흐릿하고, 집중하는 부분만 명확하게 됩니다.
이 연구가 우리가 지금 CNN이라고 부르는 것으로 진화하게 되었습니다.
2. CNN의 구조
CNN은 우리에게 익숙한 완전 연결층과 시그모이드 활성화 함수 같은 구성 요소도 들어있지만, 합성곱 층 (convolution layer)과 풀링 층 (pooling layer)이란 새로운 구성 요소도 등장합니다.
하지만 왜 이미지 인식 문제에는 완전 연결 층의 심층 신경망을 쓰지 않을까요?
이런 신경망은 작은 이미지에는 잘 작동하지만 큰 이미지에서는 많은 파라미터가 만들어지기 때문에 문제가 됩니다.
100 x 100 이미지는 픽셀 10,000개로 이루어져 있고, 만약 다음 은닉 층이 뉴런 1,000개로 만들어져도 연결이 1천만 개가 생겨버립니다. 심지어 이것은 첫 번째 은닉층에 불과합니다.
또한 심층 신경망은 그림을 1차원으로 변환하여 작업을 수행하기 때문에 데이터의 형상이 무시됩니다.
한 마디로 밀접한 픽셀은 비슷한 픽셀 값을 가지거나, 먼 픽셀은 관련이 없는 등 이런 공간적 구조를 1차원으로 펼쳐버리면 없어지게 됩니다.
CNN은 층을 부분적으로 연결하고, 가중치를 공유하여 이 문제를 해결합니다.
즉 보이는 이미지를 여러 부분으로 나누어 다시 합치는 방식입니다.
또한 2차원을 있는 그대로 집어넣어서 공간적 구조를 손실하지 않습니다.
2.1 합성곱 층 (Convolution Layer)
CNN의 가장 중요한 구성 요소입니다.
각각의 합성곱 층의 뉴런은 입력 이미지의 모든 픽셀에 연결되는 것이 아니라 합성곱 층 뉴런의 수용장에 있는 픽셀에만 연결됩니다.
또한 두 번째 합성곱 층은 첫 번째 합성곱 층의 작은 사각 영역 안에 위치한 뉴런에만 연결됩니다.
이런 구조는 네트워크가 첫 번째 은닉층에서는 작은 저수준의 특성에 집중하고, 그다음 은닉층에서는 더 큰 고수준의 특성으로 조합해 나가도록 도와줍니다.
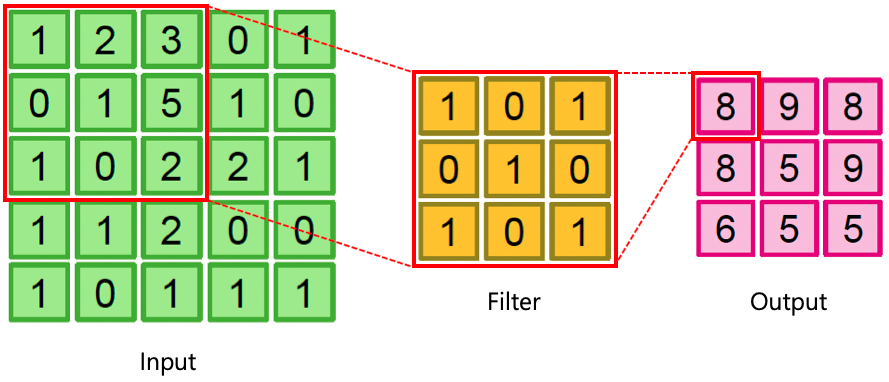
이런 식으로 말이죠. 중간에 Pool은 추후에 설명하니까 지금은 Convolution 층에만 신경 쓰시면 됩니다.
2.2 스트라이드 (stride)
스트라이드는 수용장의 위치의 간격을 결정합니다.
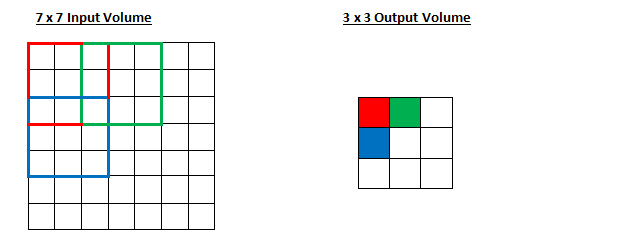
이처럼 스트라이드를 2로 설정하고, 수용장의 크기를 3x3으로 하면 출력의 크기가 3x3이 됩니다.
만약 스트라이드가 1이라면, 출력의 크기는 어떻게 될까요? 5x5가 출력됩니다.
이처럼 스트라이드를 키우면 출력의 크기는 작아집니다. 이렇게 함으로써 모델의 계산 복잡도를 크게 낮춰줍니다.
2.3 패딩 (padding)
위의 그림을 보시면 스트라이드가 2일 때, 7x7의 입력 층이 3x3의 출력층으로 변환되었죠?
이때 차원은 점점 축소됩니다.
이렇게 feature map이 작아지는 문제를 해결하기 위해 padding이라는 기법이 있습니다.
이렇게 입력하기 전에 패딩을 1로 설정하면 모두 0 (패딩 값은 설정할 수 있음)으로 넣은 다음 k+1 x k+1의 입력 값이 들어가게 됩니다.
2.4 필터, 커널 (Filter, Kernel)
보통 커널이라는 단어를 사용합니다.
커널은 수용장에 가중치를 계산하는 가중치 세트라고 생각하시면 됩니다.
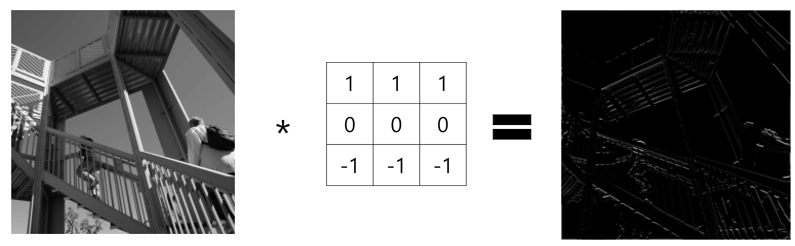
아무튼 이런 식으로 여러 가지의 커널이 있는데, 이때 수직선에 집중하는 커널은 위와 같은 이미지를, 수평선에 집중하는 커널은 아래와 같은 이지미를 출력하게 됩니다.
쉽게 생각해서 수직선을 인식하는 필터는 가운데 열만 1로 채워져 있고, 그 외에는 모두 0입니다. (다른 형태도 있긴 함)
따라서 가운데 수직선 부분을 제외하고는 수용장에 있는 모든 것을 무시할 것입니다.
혹은 가운데 수직선만 제외하고, 나머지 수직선만 인식할 수 있습니다. (이때는 커널이 가운데만 0, 나머지는 1)
이런 식으로 필터는 하나의 특성 맵 (feature map)을 만듭니다.
2.5 여러 가지 특성 맵
참고로 합성곱 층은 여러 가지 커널을 가지고 커널마다 하나의 특성 맵을 출력 합니다.
따라서 실제로는 2D가 아니라 3D로 표현됩니다.
각 특성 맵의 픽셀은 하나의 뉴런에 해당하고, 하나의 특성 맵 안에서는 모든 뉴런이 같은 파라미터(동일한 가중치와 편향, 즉 커널)를 공유하지만, 다른 특성 맵과는 다른 파라미터를 사용합니다.
이렇게 함으로써 파라미터 수를 급격히 감소시켜줍니다.
쉽게 말해서 하나의 합성곱 층이 입력에 여러 필터를 동시에 적용하여 입력에 있는 여러 특성을 감지할 수 있습니다.
특히 색깔이 있는 이미지라면 RGB라는 세 개의 채널이 있으므로, 이는 또 채널마다 다양한 특성 맵이 나오겠죠?
2.6 풀링 층 (Pooling Layer)
어떻게 합성곱 층이 작동하는지 이해했다면 풀링 층은 쉽게 이해할 수 있습니다.
풀링 층의 목적은 과도한 계산량, 메모리 사용량, 파라미터 수를 줄이고 결과적으로 over fitting의 위험을 줄여주는 축소본을 만드는 것입니다.
풀링 층의 각 뉴런은 이전 층의 수용장 안에 있는 뉴런의 출력과 연관되어 있습니다.
동일하게 크기, 스트라이드, 패딩 유형을 지정해야 하지만, 풀링 뉴런은 가중치가 없습니다.
즉, 최대나 평균 같은 계산만 하는 것이 전부입니다.
최대 풀링 층은 수용장의 픽셀 값 중에 가장 최댓값을 취하고 나머지는 버립니다.
feature map의 지나친 상세함을 줄여서 요약한 통계량을 추출해줍니다.
이때 스트라이드를 s로 설정하면 feature map은 s배만큼 줄어듭니다.
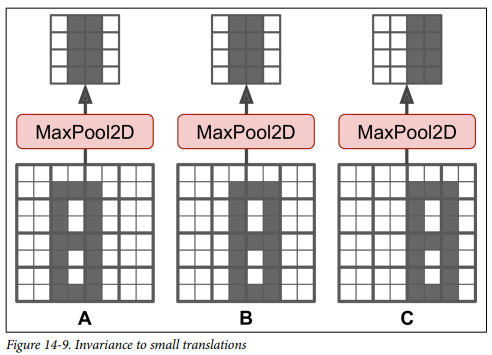
이처럼 풀링 층은 약간의 불변성도 만들어줍니다.
A, B, C 이미지가 있을 때, A와 B는 풀링을 통과해도 똑같지만, C의 출력은 다릅니다.
하지만 그럼에도 50%는 변하지 않았습니다.
이처럼 CNN에서는 풀링 층을 추가하면 전체적으로 일정 수준의 불변성을 얻을 수 있습니다.
즉, 작은 부분에 대해서 크게 영향을 받지 않을 때 유용합니다.
하지만 최대 풀링 층의 단점도 있습니다.
만약 2x2의 커널과 스트라이드 2를 사용하면 3개의 값은 버리고 1개의 값만 취하므로, 입력 값의 75%를 잃게 됩니다.
average pooling도 있습니다. average pooling은 max pooling보다는 정보 손실이 적습니다.
반면 max pooling은 의미 없는 것들을 제거하고 큰 특징만 유지하기 때문에 조금 더 명확한 신호로 학습할 수 있습니다.
일반적으로는 max pooling이 더 성능이 좋아서 최대 풀링을 사용합니다.
이처럼 풀링 층을 통과하면 좀 더 명확한 신호가 됩니다.
2.5 CNN의 구조
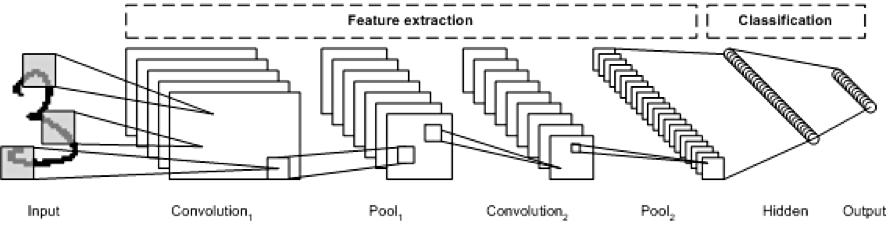
위에서 사용한 그림인데, 이제 이해가 가시나요?
일반적으로 Convolution layer을 몇 개 쌓고 (각각 활성화 함수를 뒤에 넣고), 그다음 Pooling Layer을 쌓고, 또 Convolution Layer을 쌓고(또 활성화 함수를 뒤에 넣고), 그 다음 또 Pooling Layer을 쌓습니다.
이 과정을 통해서 이미지는 점점 작아지지만, 합성곱 층 때문에 이미지는 점점 더 깊어집니다. (더 많은 특성 맵을 가짐)
그리고 마지막에는 Fully connected layer로 구성된 일반적인 신경망으로 구성되고, 분류를 하기 위해서 softmax, sigmoid layer을 통해 출력합니다.
3. CNN의 더 자세한 내용
이제 수학적 이론을 볼 차례입니다.
기본적인 convolution 연산은
\(f(i) = z(i)\circledast u = \sum_{x=-(h-1)/2}^{(h-1/2)}z(i + x)u(x)\)
입니다.
z는 입력 신호, u는 커널, h는 커널의 크기입니다.
연산은 벡터 연산을 통해서 이루어집니다.
만약 커널의 크기가 3이라면 -1에서 1까지 계산합니다.
크기가 3이면 중간의 점이 0이 되고 이를 기준으로 계산하겠네요.
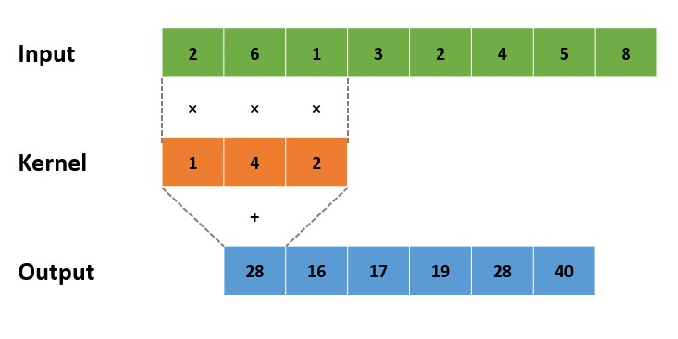
간단하죠?
2차원 컨볼루션의 경우 수식은 아래와 같습니다.
\(f(j, i) = z(i, j)\circledast u = \sum_{x=-(h-1)/2}^{(h-1/2)}\sum_{y=-(h-1)/2}^{(h-1/2)}z(j + y, i + x)u(y, x)\)
이것도 쉽죠? ㅎㅎ
3.1 컨볼루션 층의 추가적 아이디어
1. 특징 맵이 작아지는 문제를 해결하기 위해 padding
2. 영상 크기를 축소할 수 있는 스트라이드 (스트라이드를 k로 설정하면, 특징 맵은 1/k로 줄어듦)
3. 바이어스 추가
4. 활성화 함수의 연산
활성화 함수를 넣어주면 최종적으로 식은 이렇게 됩니다.
\(\tau(f(j,i))=\tau(z(j, i)\circledast u)\)
padding과 stride는 앞에서 설명했으니 굳이 설명하지 않고, 그림으로만 보여드립니다.
bias는 연산한 값에 bias 값을 더해주는 게 끝입니다.
3.2 손실 함수와 옵티마이저
CNN은 커널을 학습합니다.
DNN은 노드를 연결하는 가중치를 학습합니다.
둘의 학습 알고리즘이 다를 것 같지만 다행히도 같은 손실 함수와 같은 옵티마이저를 사용합니다.
DNN과 CNN의 중간층이 다르지만 입력과 출력은 동일하므로 같은 손실 함수를 사용합니다.
DNN은 가중치를, CNN은 커널을 최적화한다는 점만 다르지 학습 원리는 동일하므로 같은 옵티마이저를 사용합니다.
3.3 CNN이 월등한 이유
고전적인 컴퓨터 비전은 수작업 특징을 사용했습니다.
그림에서 특징을 추출해서 기존의 ML에 집어넣어서 분류를 하는 부류였죠.
하지만 딥러닝 이후로는 상황이 바뀌었습니다.
특징까지 본인이 알아내서 분류까지 본인이 스스로 합니다.
딥러닝은 특징을 학습한다고 말씀드렸었습니다.
입력에서 출력까지 전 과정을 한꺼번에 학습하므로 통째 학습 (end to end learning)이라 부릅니다.
이때 앞부분 (Convolution Layer, Pooling Layer)는 특징을 추출하고, 뒤 부분 (FC Layer)은 분류를 담당합니다.
따라서 CNN이 월등한 이유는 네 가지 이유가 있습니다.
- 통째 학습 (end to end learning) : 따로 최적화하여 붙이는 이전 방식 (Feature을 추출하고, 다시 FC에 넣는 방식) 보다 우수 (이전 Layer의 중요한 점을 다음 Layer로 넘김)
- 특징 학습 (Feature learning) : 수작업 특징보다 우수 -> 사람이 무시한 Feature도 뽑아냄
- 신경망의 깊이를 깊게 하여 풍부한 특징을 추출 -> 이때 DNN보다 오히려 파라미터는 적기 때문에 공간은 적게 먹고, 성능은 더 좋음
- 데이터의 원래 구조를 유지한 채 특징을 추출
4. 대표적인 CNN 구조 (LeNet - 5)
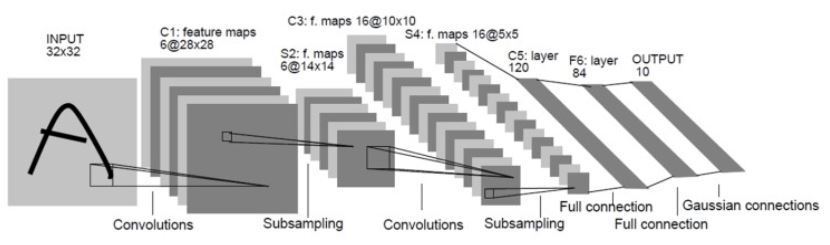
LeNet-5는 아마 널리 알려진 CNN 구조입니다.
위 그림이 LeNet-5의 구조입니다.
기본적인 구조는 C-P-C-P-C-FC-FC입니다.
(C : Convolution Layer, P, S : Pooling Layer, FC : Fully Connected Layer)
자세한 구조는 아래와 같습니다.
| 층 | 종류 | 특성 맵 | 크기 | 커널 크기 | 스트라이드 | 활성화 함수 |
| 입력 | 입력 | 1 | 32 x 32 | - | - | - |
| C1 | 합성곱 | 6 | 28 x 28 | 5 x 5 | 1 | tanh |
| P2 | 평균 풀링 | 6 | 14 x 14 | 2 x 2 | 2 | tanh |
| C3 | 합성곱 | 16 | 10 x 10 | 5 x 5 | 1 | tanh |
| P4 | 평균 풀링 | 16 | 5 x 5 | 2 x 2 | 2 | tanh |
| C5 | 합성곱 | 120 | 1 x 1 | 5 x 5 | 1 | tanh |
| FC6 | 완전 연결 | - | 84 | - | - | tanh |
| 출력 | 완전 연결 | - | 10 | - | - | RBF |
5. 요약
이번에는 간단히 CNN에 대해 알아봤습니다.
CNN은 Convolution Neural Network의 줄임 말으로써, 인간의 시각 기능을 응용한 DNN입니다.
시각 신경의 각 뉴런은 각각 특정한 특징에만 반응하고, 이 반응한 특징들을 하나로 합쳐서 주위를 인식합니다.
CNN도 마찬가지로 이미지를 각 Convolutaion Layer의 뉴런이 Kernel이라는 특징을 통과해 특정한 특징만 가지고 있는 Feature Map을 가지게 되고, 이러한 Feature Map을 통해서 인식을 하게 됩니다.
하지만 가면 갈수록 Feature Map이 작아진다는 문제점이 있고, 이를 막기 위해 Padding 기법이 있습니다.
Padding 기법은 주위를 0 또는 주위 값으로 덧댑니다.
또한 모델의 계산 복잡도를 낮춰주기 위해서 stride를 설정하는 방법도 있었습니다.
Convolution Layer만 있다면, 과대 적합이 심할 수 있어서, 지나친 상세함을 줄이는 풀링 층도 있었습니다.
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] RNN과 LSTM (0) | 2022.04.17 |
|---|---|
| [머신러닝 - 이론] CNN 시각화, CNN 성능 향상, 전이 학습 (CNN Visualization, CNN Improve Performanc (0) | 2022.04.10 |
| [머신러닝 - 이론] 지금까지의 내용 정리 (0) | 2022.04.09 |
| [머신러닝 - 이론] 최적의 하이퍼 파라미터 찾기, 모델을 다듬는 방법 (Find Hyper Parameter, Fine-Tune Model) (0) | 2022.04.09 |
| [머신러닝 - 이론] 딥러닝의 학습 전략 (Learning Strategy of Deep Learning) (0) | 2022.04.09 |