강화 학습을 잘 모를 수 있지만, 알파고를 모를 수는 없습니다.
알파고는 강화 학습을 통해 학습된 모델입니다.
이처럼 강화학습은 요즘 가장 흥미진진한 분야이자 가장 오래된 분야 중 하나입니다.
사람은 주위를 센싱하고 인식하여 적절한 행위를 통해 환경과 상호작용합니다.
인공지능 제품도 비슷한 과정을 수행해야 쓸모가 있습니다.
1. 에이전트 (Agent)
일상생활에서 에이전트 (Agent)란 특정한 일을 대행해주는 사람을 뜻합니다.
강화 학습에서의 에이전트는 관측을 하고 주어진 환경에서 행동을 합니다. 그리고 그 결과로 보상을 받습니다.
에이전트의 목적은 보상의 장기간 기대치를 최대로 만드는 행동을 학습하는 것입니다.
목적지에 도착하면 양의 보상을 받고, 시간을 낭비하거나 잘못된 방향으로 향하면 음의 보상을 받습니다.
꼭 에이전트가 물리적으로 움직여야 하는 것은 아닙니다. 목표 온도를 맞추어 에너지를 절약하면 양의 보상을 받고, 사람이 온도를 조작할 필요가 생기면 음의 보상을 받는 스마트 온도 조절기일 수 있습니다.
그러므로 에이전트는 사람의 요구를 예측하도록 학습되어야 합니다.
또한 주식시장의 가격을 관찰하고 얼마나 사고팔아야 할지 결정할 수 있습니다.
또한 양의 보상이 전혀 없을 수도 있습니다. 에이전트가 미로 속을 움직인다면 매 타임 스텝마다 음의 보상을 받기 때문에 가능한 한 빨리 탈출구를 찾아야 합니다.
지능 에이전트는 다음과 같은 구조를 가집니다.

지능 에이전트의 라이프 사이클은 다음과 같습니다.
- 문제 정의
- 비즈니스 정의, 데이터 수집
- 모델 제작 (에이전트 제작)
- 모델 설계, 모델 학습, 모델 평가
- Deploy (에이전트와 환경의 상호작용)
- 지식 베이스 부착, UI 부착, 현장 평가
단계 1 : 문제 정의에서는 비즈니스 정의 (음식 인식 앱의 경우, 음식의 범위, 음식의 계층 구조 등을 결정)
데이터 수집 (현장을 대변하는 다양한 음식 영상 수집, 데이터가 가장 중요한 산출물)
단계 2 : 모델 제작에서는 CNN, RNN, DNN, RL중 무엇을 사용할 건지 결정하고, 테스트합니다.
단계 3 : Deploy에서는 해당 모델 (에이전트)를 실제 현장에 배치합니다.
2. 강화 학습 (Reinforcement Learning)
인간과 동물은 환경의 상태를 보고 자신에게 유리한 행동을 결정하고 실행합니다.
행동에 따른 결과가 좋으면 기억했다가 반복하고, 결과가 나쁘면 회피합니다.
대표적인 예시로 자전거 타기, 바둑 등등이 있습니다.
즉, 미리 답을 알려주지 않습니다.
기존의 CNN, RNN은 훈련 집합과 답을 미리 줬었죠?
하지만 강화 학습에는 미리 답을 알려주지 않습니다.
(행동 -> 상태 변화 -> 보상의 학습) 이렇게 사이클이 돕니다.
에이전트가 행동을 결정하기 위해 사용하는 알고리즘을 정책 (policy)라고 합니다.
예를 들어 관측을 입력받고 수행할 행동을 출력하는 신경망이 정책이 될 수 있습니다.
이때 정책을 결정하는 대표적인 두 가지 방법이 있습니다.
- 탐험형 정책 (exploration policy)
- 탐험형 정책은 처음부터 끝까지 무작위로 선택하는, 즉 매번 다른 경우의 수를 선택하고 가장 성능이 좋은 조합을 고르는 방법입니다.
- 이용형 정책 (exploitation policy)
- 기존의 경험을 통해서 가장 최대의 보상을 얻을 수 있는 행동을 수행하는 것을 의미합니다.
따라서 이용형 정책을 하기 위해서는 경험을 쌓아야 하므로 탐험형 정책이 먼저 수행되어야 합니다.
탐험을 통해 얻은 결과가 항상 최상일 수는 없기에 이 부분에서 낭비가 되고, 풍부한 경험이 있어야만 좋은 선택을 할 수 있지만, 경험을 풍부하게 만들기 위해서는 새로운 시도를 해야 하고, 새로운 시도는 항상 위험 부담을 가지고 있습니다.
충분히 에피소드가 길다면 해법이 단순합니다.
강화학습에서 게임을 시작하여 마칠 때까지 기록을 에피소드라 부릅니다.
충분히 긴 에피소드로부터 최적의 정책을 알아낼 수 있습니다.
하지만 수시로 확률이 바뀐다던가, 돈과 시간이 충분하지 않은 경우가 태반입니다.
따라서 탐험형 정책과 탐사형 정책의 균형이 매우 중요합니다.
이때 정책의 대표적인 알고리즘이 있습니다.
바로 랜덤 알고리즘과 그리디 알고리즘입니다.
이름만 들어도 랜덤은 탐험형이고 그리디는 탐사형인걸 알 수 있죠?
e - 탐욕 알고리즘은 기본적으로 탐사형에 치우쳤는데, e 비율만큼 탐험을 적용하여 탐사와 탐험의 균형을 추구합니다.
또 다른 예시로는 몬테카를로 방법이 있습니다.
몬테카를로 방법은 어떤 현상을 난수로 생성하여 시뮬레이션하는 기법입니다.
예를 들어 우주 전체의 모든 원자를 합한 수보다 더 많은 조합과 배열이 가능하다고 알려진 바둑을 어떻게 알파고가 이겼을까요?
알파고도 모든 경우의 수를 내놓는 것은 불가능하기 때문에 몇몇 개의 표본을 뽑아내 승률을 추측했습니다.
이처럼 난수를 통해서 확률의 근사치를 알아내는 방법이 몬테카를로 방법입니다.
아무튼 강화 학습에서 보상을 최대화할 수 있는 방향으로 탐험과 이용 사이의 적절한 균형을 맞추는 데 사용되는 의사 결정 프로세스가 바로 마르코프 결정 프로세스입니다.
2.1 마르코프 결정 프로세스 (MDP : markov decision process)

이러한 문제가 있을 때 MDP는 상태의 종류, 행동의 종류, 보상의 종류를 지정하고, 행동을 취했을 때 발생하는 상태 변환을 지배하는 규칙을 정의합니다.
- 상태 집합 : S = {s_1, s_2, ... , s_l}
- 행동 집합 : A = {a_1, a_2, ... , a_m}
- 보상 집합 : R = {r_1, r_2, ... , r_n}

상태 전이 확률이란 어떠한 행동을 했을 때 상태 s`로 변화되는 확률을 말합니다.
결정론적 환경(100% 확률로 새로운 상태가 정해지는 환경)에서의 상태 전이 확률은 다음과 같습니다.
이때 P(s` = 2, r = 0 | s = 1, a = 2) = 1.0은 무엇을 의미할까요?
이는 조건부 확률입니다.
상태 1에서 행동 2를 선택하면, 새로운 상태 2로 전환되고 보상이 0일 확률이 1이라는 뜻입니다.
하지만 스토캐스틱 환경(확률 분포에 따라 새로운 상태가 다르게 정해지는 환경)에서는 정확한 값을 나타낼 수 없습니다.
이때는 상태 전이 확률 분포라고 칭하며 다음과 같습니다.
상태 전이 확률 분포는 마르코프 결정 프로세스에 속하는 집합들로 확률을 나타낸 것이라 볼 수 있습니다.
상태 전이 확률 분포 : \(P(s`,r|s,a),\forall s \epsilon S,\, \forall a \epsilon A,\, \forall r \epsilon R\)
3. 최적 정책과 가치 함수, 벨만 기대 방정식, 동적 프로그래밍
- 최적화의 목표
- 누적 보상의 최대화입니다. 당장은 손해가 나더라도 전체 과정에 걸쳐 누적 보상액을 최대화해야 합니다.
- 학습 알고리즘이 알아내야 하는 것
- 누적 보상을 최대화하는 최적 정책
- 품질을 평가하는 함수
- 가치 함수
- 학습 알고리즘
- 동적 프로그래밍, Sarsa, Q 러닝, DQN 등
3.1 최적 정책
이때 정책을 확률 분포로 나타내면 다음과 같습니다.
정책 : \(\pi (a|s)= P(a|s), \,\forall s \epsilon S,\, \forall a \epsilon A \)
이때 P(a = i | s = j)는 상태 변수 j라는 값일 때, 행동 변수 a가 i라는 값을 취할 확률입니다.
이때 \(\hat{\pi}\)는 최적 정책을 뜻합니다.
예를 들어서 3개의 손잡이 중 2번 손잡이의 승률이 최대라고 하면
\(\hat{\pi}\)는 P(a = 0 | . ) = 0, P(a = 1 | . ) = 1, P(a = 2 | . ) = 0이 됩니다.
문제가 단순하다면 최적의 정책을 찾기 쉽지만, 보통은 그렇지 않으므로 가치 함수를 통해서 정책의 품질을 평가합니다.
3.2 가치 함수
가치 함수 : \(v_\pi(s), \forall s \epsilon S\)로 정의하며,
학습 알고리즘은 \(v_\pi(s)\)를 최대화하는 최적 정책 \(\hat{\pi}\)를 찾는 것입니다.
\(\hat{\pi} = argmax_{\pi} \,v_{\pi} (s), \,\forall s \epsilon S \)
이때 가치 함수는 다음과 같이 계산합니다.
\(v_\pi(s)=E(\sum r|s)= \sum_{z} P(z)r(z),\,\forall s \epsilon S\)
z는 s에서 출발하는 모든 에피소드를 의미합니다.
아래는 가치 함수를 계산하는 예시입니다.


즉, 어떤 state S에서 행동하는 모든 action, episode에 대해서 확률과 보상을 곱해서 모두 더하면 해당 정책에 대한 가치가 나옵니다.
따라서 가능한 모든 정책 안의 정책인 pi_i 정책에 따라 s에서 어떤 a을 취할 확률과 그에 따른 보상을 모두 곱한 후 더한게 pi_i의 가치입니다.
이때 i는 1부터 모든 경우의 수 n까지 다 계산합니다.
따라서 최적 정책은 모든 n개의 가치 함수 중에 가치 함수가 최대가 되는 정책을 구합니다.
따라서 신경망과 마찬가지로 \(\pi_1\)로 초기화 한 다음, \(\pi_1\)을 개선한 \(\pi_2\)를 구하고, 또 ... 반복하다가 결국 최적 정책인 \(\hat{\pi}\)에 수렴하게 됩니다.
3.3 벨만 기대 방정식
실제 세계에서는 가치 함수를 계산하기도 힘듭니다.
이때 가치 함수를 계산하기 위해서 앞으로 받을 모든 보상에 대해 고려해야 합니다.
이는 state가 많은 환경에서는 매우 비효율적입니다.
따라서 하나의 수식으로 풀어내는 것보단 여러 번의 연속적인 계산으로 가치 함수의 값을 알아내는 방법이 효율적입니다.
이러한 방법을 쓰는 것이 바로 벨만 기대 방정식입니다.
이미 저장되어 있는 다음 상태의 가치 함수를 이용해서 현재 상태의 가치 함수를 계산합니다.
너무 수식 쓰기 힘들어서 가져왔습니다..ㅠㅜ
벨만 기대 방정식(할인율, 감가율을 적용한)은 아래와 같습니다.
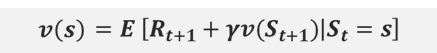
R은 어떤 행동을 취했을 때 받는 보상입니다.
이를 유도하는 과정은 아래와 같습니다.
참고로 G_t는 반환 값입니다.

감가율(γ)을 곱해주었는데, 감가율은 뒤에서 설명하겠습니다.
아무튼 우리가 보기 쉽게 바꾸자면 아래와 같습니다.

따라서 벨만 기대 방정식의 예시는 아래와 같습니다.
참고로 감가율은 고려하지 않았습니다.
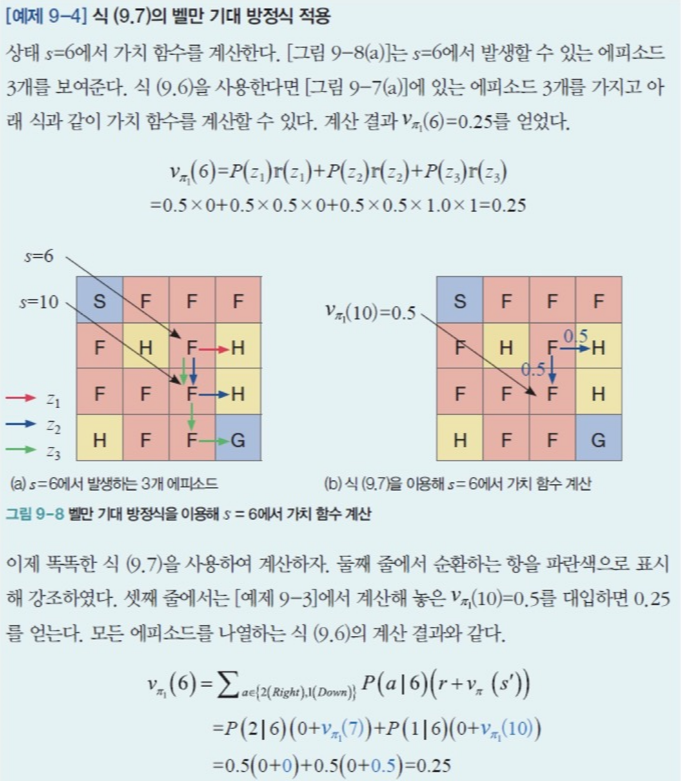
위에서 설명한 가치 함수는 '상태 가치 함수(state value function)'입니다. 즉 이 함수를 통해서 다음 상태들의 가치를 판단할 수 있고, 이를 바탕으로 더 높은 가치를 가지고 있는 다음 상태로 가기 위한 행동을 선택해야 합니다.
하지만 a라는 다음 상태의 가치가 높아서 a`이라는 행동을 하려고 했는데, a`의 확률보다 b`의 확률이 높아서 b` 행동을 해버렸고, 그 결과로 b 상태로 가버렸다고 생각해봅시다.
즉, 상태 가치 함수는 어떤 상태에 대한 가치만 나타낼 수 있고, 행동에 대한 가치를 나타내지 않습니다.
따라서 '행동 가치 함수 (action value function), Q함수'는 특정 상태 s에 대해서 행동 a를 취했을 때 취하는 가치에 대해 알 수 있습니다.
따라서 행동 가치 함수, 즉 Q함수는 아래와 같습니다.
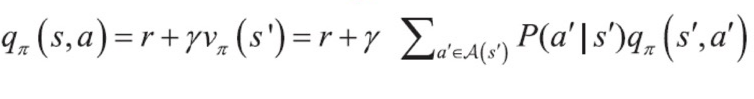
3.4 동적 프로그래밍
따라서 동적 프로그래밍을 사용하여 최적의 정책이나 최적의 가치를 찾아내는 알고리즘은 다음과 같습니다.


하지만 동적 프로그래밍은 마르코프 결정 프로세스를 알아야만 적용이 가능하다는 한계가 있습니다.
초기에는 마르코프 결정 프로세스를 모르므로 그냥 확률 기반으로 결정해야 합니다.
또한 표를 사용하기 때문에 크기가 작은 문제에 국한하여 적용이 가능합니다.
3.5 감가율
누적 보상액 (accumulating reward), r(z)는 현재 순간 t에서 시작하여 에피소드가 끝날 때까지 발생한 보상의 총액입니다.
감가율 (discount rate, γ)는 미래에 발생하는 보상의 가치를 일정 비율 삭감하는 역할입니다.
따라서 감가율을 적용한 벨만 기대 방정식은 위의 그림과 마찬가지로
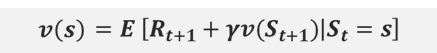
입니다.
4. 요약
강화 학습이 제일 어렵네요 ,,
강화 학습은 어떤 에이전트를 통해서 하는 학습입니다.
에이전트는 상황에 따라 행동을 하고 보상을 받습니다.
이때 보상이 최대화되는 방향으로 행동을 하는 것이 목표입니다.
하지만 보상이 얼만큼 되는지, 좋은지 나쁜지는 알 수 없으므로, 일단 행동을 해봐야 합니다.
행동을 하는 방법이 탐험형과 이용형이 있습니다.
탐험형은 무작정 찾는 것이고, 이용형은 현재까지의 에피소드를 바탕으로 제일 좋은 행동을 합니다.
하지만 보상을 최대화하기 위해서는 탐험형과 이용형을 적절히 이용해야 합니다.
이러한 문제를 형식화한 것이 마르코프 결정 프로세스입니다.
특정 상태 s를 받고, 어떤 행동 a를 한다면, 환경은 새로운 상태 s`을 주고, 보상인 r을 줍니다.
이러한 것을 tree형태로 만든 것이 마르코프 결정 프로세스입니다.
에이전트가 현재 상태에서 다음 상태로 가는 것을 상태 전이라고 부르고, 이를 확률론에 기반하여 상태 전이 확률로 만들 수 있습니다.
즉 어떤 상태에서 어떤 행동을 취하면, 새로운 상태 s`으로 가고, r 보상을 받는 것에 대한 확률입니다.
아무튼 최대 보상을 받기 위한 일련의 과정이 있습니다.
이때 상태 s가 있다면, a라는 행동을 하게 정책을 만들어 놓았습니다.
우리가 해야 할 것은 누적 보상의 최대화이고, 학습 알고리즘은 누적 보상이 최대화가 되는 최적 정책을 찾아야 합니다.
이때 최적 정책은 어떻게 알아낼까요? 바로 가치 함수를 통해서 알아냅니다.
가치 함수가 최대가 되는 정책을 학습 알고리즘이 알아내야 합니다.
가치 함수는 어떤 s에서 출발하는 모든 에피소드 z에 대한 에피소드 z로 갈 확률 * z의 보상을 더합니다.
가치 함수 하나를 구하기 위해 모든 에피소드에 대한 확률과 보상을 다 구해야 할까요?
당연히 그건 너무 비효율적입니다.
따라서 벨만 기대 방정식이란 것을 만들어서 다음 상태의 가치 함수와 현재 상태의 가치 함수에 대한 방정식으로 현재 상태에 대한 가치 함수를 구합니다.
그렇다면 최종 상태의 가치 함수에서 DP 알고리즘으로 쭉 올라오면 되겠죠?
아무튼 보상들의 단순 합으로 가치를 판단하기엔 시간 개념을 적용할 수 없어서, 할인율을 이용한 반환 값을 이용합니다.
이때, 특정 행동을 할 확률 P(a|s)와 a를 통한 보상 s`을 곱해서 나오는 기댓값을 알아내는 게 벨만 기대 방정식이 되겠습니다.
근데 이때, a라는 행동을 해야 최고의 보상을 얻는데, 확률 때문에 b로가면 손해입니다.
벨만 기대 방정식은 어떤 상태에 대한 가치를 나타낼 수 있지, 상태와 행동에 대한 가치를 나타낼 수 없습니다.
따라서 나온 게 Q함수, 즉 행동 가치 함수가 되겠습니다.
감사합니다.
지적 환영합니다.