1. 데이터의 종류, 분별력
앞의 iris 데이터에서 특징은 총 4개가 있었습니다.
이때 특징을 4차원 공간에서 보면, 레이블에 따라 몇몇 데이터는 뭉쳐져 있고, 몇몇 데이터는 떨어져 있는 것을 알 수 있습니다.
물론 4차원 공간을 볼 순 없지만, 3차원 공간으로는 볼 수 있습니다.
이때 특징에 따라 같은 레이블이 뭉쳐져 있고, 다른 레이블과의 거리가 멀다면 이 특징은 분별력 (descriminating power)이 뛰어나다고 볼 수 있습니다.
이때 다차원의 특징은 거리를 바탕으로 계산합니다.
또 다른 데이터로는 영상 데이터가 있습니다.
대표적으로 MNIST라는 숫자를 필기한 데이터가 있습니다.
이때는 화소 값이 특징 벡터입니다.
또 다른 영상 데이터는 얼굴 데이터셋이 있습니다.
어떤 데이터가 있으면 여기서 특징을 추출하는 것이 중요합니다.
이때 분별력이 높은 특징을 추출해야 합니다. 왜냐면 그래야 머신러닝이 분별력 있는 학습을 하기 때문입니다.
특징 값의 종류는
- 수치형 특징
- 거리 개념이 있음
- 실수 또는 정수 혹은 이진값
- 길이 : 3, 넓이 : 4 같은 특징
- 범주형 특징
- 순서형
- 학점, 수능 등급 등
- 거리 개념이 있으므로 순서대로 점수를 부여하면 수치형으로 취급 가능
- 학점, 수능 등급은 범주가 있음, 1등급 ~ 9등급 같은 범위
- 이름형
- 혈액형, 지역 등으로 거리 개념이 없음
- 보통 원핫 코드로 표현함
- 범위가 정해져 있지 않음
- 순서형
2. 성능 측정
성능을 측정할 때 객관적인 성능 측정이 중요합니다.
학습 데이터에 대해서 예측을 하면 뭘 하나요.. 학습 데이터로 학습을 했고, 또 학습 데이터를 예측하면 당연히 모두 제대로 나오겠죠??
이때 중요한 게 바로 일반화 (generalization) 능력입니다.
일반화 능력이란 학습에 사용되지 않았던 새로운 데이터에 대한 성능입니다.
가장 좋은 방법은 실제 현장에 배치하고 성능을 측정하는 건데,,,,,,아무래도 무리가 있겠죠?
그래서 보통 주어진 데이터를 분할해서 사용합니다.
이때 성능을 측정하기 위해 혼동 행렬(confusion matrix)이란 것을 사용합니다.
혼동 행렬은 부류 별로 옳은 분류와 틀린 분류의 개수를 기록한 행렬입니다.
이때 이진 분류를 한다고 하면, 긍정 값과 부정 값으로 나뉘겠죠?
검출하고자 하는 것이 긍정(환자가 긍정, 정상인이 부정)이고, 참/거짓은 머신러닝이 제대로 된 예측을 했는지를 보여줍니다.
| 그라운드 트루스 | |||
| 긍정 | 부정 | ||
| 예측값 | 긍정 | TP | FP |
| 부정 | FN | TN | |
참 긍정 (TP), 거짓 부정 (FN), 거짓 긍정 (FP), 참 부정 (TN)입니다.
이때 성능 측정 기준은
- 정확률 (accuracy)
- 맞힌 샘플 수 / 전체 샘플 수
- 정밀도 (precision)
- TP / TP + FP
- 즉 모델이 맞다고 예측한 것 중에 정말로 뭐가 맞는지를 알려줍니다.
- 코로나 양성 판정일 때 진짜일 확률입니다.
- 재현률 (recall)
- TP / TP + FN
- 즉 실제로는 긍정인 것 중에 모델이 얼마나 제대로 측정했는지를 알려줍니다.
- 이미 코로나 양성 판정을 받은 사람 중 모델이 예측했을 때, 얼마나 제대로 측정하는지를 알려줍니다.
3. 데이터 쪼개기
주어진 데이터를 적정 비율로 훈련, 검증, 테스트 집합으로 나눕니다.
보통 모델을 선택하기 위해서는 훈련/검증/테스트로 나누고,
모델을 선택하지 않으면 훈련/테스트로만 나눕니다.

간단히 데이터셋을 0.6 : 0.4로 나눴습니다.
이때 교차 검증은 데이터를 교차적으로 검증하는 것입니다.
훈련/테스트 집합으로 나누는 것은 한계가 있습니다.
왜냐하면 우연히 높은 정확률을 가진 테스트 집합, 혹은 우연히 낮은 정확률이 발생할 수 있기 때문입니다.
따라서 학습 데이터를 k개의 부분 집합으로 나누고 k-1개를 학습 후, 남은 하나의 집합에 대하여 성능을 측정합니다.
이렇게 한 후 k개의 성능을 평균하여 신뢰도를 높이는 것이 k-겹 교차 검증(k-fold cross validation)입니다.

보시면 정확률이 들쭉날쭉합니다. 이렇게 한 번만 시도하는 프로그램의 위험성을 잘 보여줍니다.
k를 크게 하면 신뢰도는 올라가지만, 실행 시간이 더 걸립니다.
4. 특징 공간을 분할하는 결정 경계
인공지능은 철저히 수학에 의존합니다.
아무튼 모델은 아무나 만들 수 있지만, 철저한 수학적 원리, 동작 원리에 대한 이해가 없으면 한계가 드러납니다.
샘플은 feature vector로 표현되며, feature vector는 feature space의 한 공간에 해당합니다.
어떤 방법은 이 feature vector를 또 다른 feature space에 여러 차례 변환해서 최종적으로 feature space를 분할하여 부류를 결정합니다.
이때 특징 공간을 분할하는 것이 결정 경계 (decision boundary)입니다.
이때 결정 경계를 정하는데 중요한 고려 사항이 있습니다.
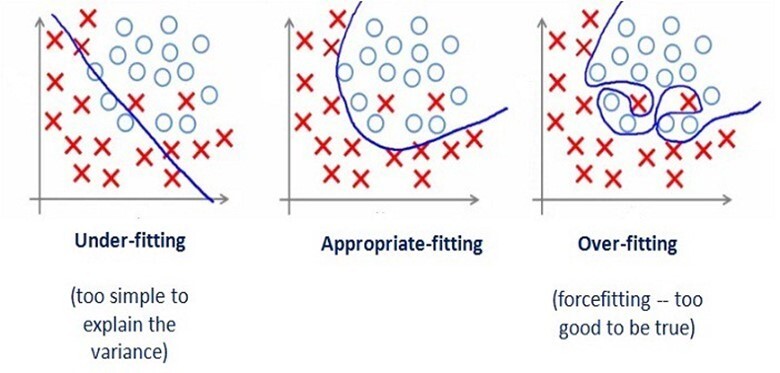
이 그림처럼 과대 적합 (over-fitting)이 일어나면 너무 복잡한 결정 경계를 만들게 됩니다.
이때 훈련 집합에 대해서는 성능이 뛰어나지만, 새로운 집합에 대해서는 성능이 너무 낮습니다.
즉, 일반화 성능이 낮습니다.
over-fitting을 막는 방법은 추후에 알려드리겠습니다.
5. 요약
ML vs DL : hand-crafted feature vs feature learning
데이터 이해 : 특히 다차원의 특징 공간에 대해 이해해야 합니다.
특징(feature) 추출/표현은 좋은 Discriminating power이 있어야 합니다.
중요한 단어는
confusion matrix : 실제 분류와 예측 분류를 갖는 행렬입니다.
measurement : accuracy, precision, recall입니다.
accuracy : 맞힌 샘플 수 / 전체 샘플 수
precision : TP / TP + FP
recall : TP / TP + FN
Data sprlit : train/validation/test -> data bias를 막기 위해
k-fold cross validation -> 우연히 높은 정확률을 보일 수 있기 때문에, k개로 나눈 후 k-1개로 학습, 하나로 검증을 거쳐 평균을 내서 신뢰도를 높이는 방법
Decision boundary issue : over fitting, generalization
over fitting -> 학습 데이터에 너무 과중하게 학습
generalization -> 얼마나 새로운 데이터에 잘 적응하는가
감사합니다.
지적 환영합니다.