이제부터 머신러닝의 꽃인 딥러닝에 대해 알아보겠습니다.
사실 제 생각엔 딥러닝을 하기 전에 지도, 비지도 학습을 먼저 공부하고, 수학적 이론을 쌓은 다음에 공부해야 하는 게 맞다고 생각합니다.
근데 시험 공부랑 겹쳐서... 어쩔 수 없이 딥러닝을 먼저 하게 되네요...
추후에 다른 머신러닝 알고리즘도 올리겠습니다.
1. 인공 신경망이란?
인간의 뇌는 신경의 망들로 이루어져 있습니다.
뉴런은 뇌의 정보처리 단위입니다. 처리한 정보를 다른 뉴런으로 옮기고, 받은 뉴런은 자신이 연산을 처리하고 또 다른 뉴런에게 보냅니다.
인간의 뇌는 고도의 병렬 처리기입니다.
하지만 컴퓨터는 아주 빠른 순차 명령 처리기죠.
아무튼 인공 신경망은 생물의 신경망에서 원리를 얻었지만, 실제 구현은 많이 다릅니다.
인공 신경망을 ANN (Artificial Neural Network)라고 하고, ANN을 위한 다양한 이론과 기술들이 나왔습니다.
2. 퍼셉트론
지금으로는 많이 낡은 기술이지만 신경망 공부에서 매우 중요한 기술입니다.
퍼셉트론이 다층 퍼셉트론과 딥러닝의 핵심 구성 요소이기 때문입니다.
또한 퍼셉트론은 단순한 모델이기 때문에 머신 러닝의 용어와 원리를 이해하는데 적합합니다.
2.1 퍼셉트론의 구조
퍼셉트론은 입력층과 출력층으로 이루어져 있습니다. 이때 출력층은 한 개의 노드입니다.
입력층은 d+1개의 노드입니다. (이때 d는 특징 벡터의 차원)
특징 벡터 : \(x=(x_1, x_2, ... , x_d)\)
이때 i번째 입력 노드와 출력 노드는 가중치 \(w_i\)를 가진 edge로 연결됩니다.
쉽게 말해서 i번째 입력 노드와 출력 노드는 어떤 가중치로 연결되어 있다고 보시면 됩니다.

퍼셉트론은 위와 같은 구조를 가지고 있습니다.
간단하죠? constant는 bias 노드입니다.
이때 퍼셉트론은 입력 노드와 가중치를 곱해서 출력 노드로 전달합니다.
이때, 0번째 입력 노드는 1인 바이어스 노드입니다.
이때 모든 \(x_i\)와 \(w_i\)를 다 곱해서 더한 후, 활성화 함수라는 함수에 넣어주면 됩니다.

이번에는 활성화 함수는 위의 그림과 같이 계단 형태입니다.
실제로 활성화 함수의 종류는 매우 다양합니다.
즉, 결과 값이 0보다 크면 1, 아니라면 0을 출력합니다.
아주 간단하게 뉴런이 활성화하는 과정을 모방했습니다.
이를 수식으로 나타내면,
\(o=\tau(s)=\tau(\sum_{i=1}^{d}w_ix_i + w_0)\)
이 되겠습니다. 간단하죠?
암튼 보통은 행렬을 이용해서 표현하므로 다시 간결한 표현을 쓰겠습니다.
w와 x는 1*d 행렬(x의 전치 행렬, x^T는 d*1 행렬)
고로 wx^T는 1x1 행렬으로서 스칼라 값입니다.
또한 바이어스를 첫 번째 요소로 추가해서
x를 1 * (d + 1) 행렬 \(x_0, x_1, ... , x_d\), w를 1 * (d + 1) 행렬로 확장하면
\(o=\tau(wx^T)\)로 쉽고 간단하게 표현할 수 있습니다.
w와 x라는 행렬을 곱해서 활성화 함수에 넣어준 모습입니다.
2.2 퍼셉트론의 학습 원리 (손실 함수)
실제 상황에서는 데이터만 주어지고, 가중치는 주어지지 않습니다. 따라서 데이터로부터 가중치를 알아내야 합니다.
이때, 가중치를 알아내는 과정이 학습이라고 생각하시면 됩니다.
신경망의 학습 방법은 처음부터 제대로 된 가중치를 찾는 것이 아닌, 조금씩 나은 방향을 찾아 개선해 나가는 절차입니다.
이때 신경망은 철저히 수학에 의존하며, 신경망의 학습은 최적화의 문제이고, 최적화 대상은 신경망의 가중치입니다.
이때 어떤 기준을 통해서 가중치를 최적화할까요??
바로 손실 함수 (loss function)입니다.
추후에 자세한 이론을 설명드리지만, 우선 이해하기 위해서는, 손실 함수는 모델이 예측한 값과 실제 값의 차이를 나타내는 함수라고 생각하시면 됩니다.
만약 가중치 w가 모든 샘플을 맞추면 손실 함수인 J의 J(w)는 0입니다.
고로 w가 틀리는 샘플이 많을 수록 J(w)의 값은 큽니다.
만약 w가 틀린다고 가정해봅시다.
손실 함수는 \(J(w)=\sum_{x\epsilon I} -y(wx^T)\)라고 정의합니다.
(참고로 x는 데이터, y는 데이터의 레이블 값입니다.)
x가 +1의 부류라면 ( 즉 y = 1이라면), 퍼셉트론의 출력 \(wx^T)\)은 음수입니다. w는 -1을 내놓을 테니까요.
그렇게 되면 \(y(wx^T)\)는 양수 값이 됩니다.
한 번 x가 -1의 부류일 때도 계산해보세요. 아마 양수 값이 나올 겁니다.
이처럼 손실 함수는 예측 값이 틀릴 때, 높은 값을 가지게 되어있습니다.
하지만 무작정 w를 바꿔가면서 손실 함수를 낮추면서 w를 갱신할 수 없는 법입니다.
손실 함수를 낮추는 법에도 다양한 기법들이 있는데, 다음 2.3 챕터에서는 그중 가장 기본적인 기법에 대해 알려드리겠습니다.
2.3 손실 함수의 최소점 찾는 기법 (경사 하강법)
2022.07.28 - [Computer Science/머신러닝] - [머신러닝 - 이론] 경사 하강법 (Gradient Descent)
경사 하강법 (gradient descent)는 손실 함수 J의 최저점이 되는 w를 찾는 기법입니다.
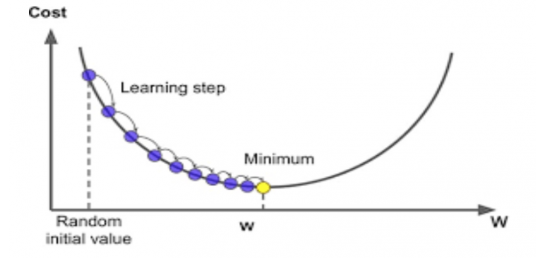
이 그림을 보시면 이해가 되시나요? w가 하나일 때의 경우입니다.
보시다시피 함수는 J입니다. 경사하강법은 w를 넣고, 어디로 가야 최저점으로 가는지를 알려줍니다.
딱 보시면 미분이 떠오르시죠? 기울기가 음수이면 w를 증가시키고, 기울기가 양수이면 w를 감소시키면 됩니다.
즉 경사 하강법은 미분을 이용하여 최적해를 찾는 기법입니다.
이를 함수로 나타내면
\(w_1 = w_1 + \rho(-\frac{\partial J}{\partial w_1})\)
이 됩니다!
J를 w에 대하여 미분한 다음 음수를 취하면 내가 가야할 방향을 제시해줍니다.
이때 방향은 알 수 있지만, 얼만큼 가야 하는지에 대한 정보가 없기 때문에 학습률인 \(\rho\)를 곱해서 조금씩 이동합니다.
만약에 매개변수가 여러개라면 편미분으로 구한 그레디언트를 사용하여 계산합니다.
(매개변수 별로 독립적으로 미분)
그러면 식은 이렇게 됩니다.
\(w = w + \rho(-\triangledown w)\)이 되고,
\(\triangledown w= (\frac{\partial J}{\partial w_0}, \frac{\partial J}{\partial w_1},\frac{\partial J}{\partial w_2},\cdots \frac{\partial J}{\partial w_d})\)
이 됩니다!!
뭔가 수식이 복잡한데, 그냥 매개변수 별로 편미분해서 그거로 계산한다고 생각하시면 됩니다!
이때 위에서 손실 함수의 함수식을 말씀드렸죠?
그 식을 매개변수 \(w_i\)로 미분해봅시다!
\(\frac{\partial J}{\partial w_i} = \sum_{x \epsilon I} \frac{\partial(-y(w_0 + w_1x_1 + \cdots w_ix_i + \cdots w_dx_d))}{\partial w_i} = \sum_{x \epsilon I} -yx_i\)
라는 식이 튀어나옵니다. \(w_i\)에 대하여 다른 w는 모두 상수므로 0이 되고, 결국 \(w_ix_i\)만 미분되어 \(x_i\)만 남게 됩니다.
고로 뒤의 식이 나오게 됩니다!!
이를 경사 하강법의 공식에 넣으면,
\(w =w + \rho \sum_{x \epsilon I} yx\)
이 나오게 됩니다!
근데 yx가 어떻게 방향을 정하는지는 저도 잘 모르겠습니다.....ㅠㅠ
일단 교수님께 문의는 해놨습니다........
알아보니까 단순화하기 위해서 저런 형태를 썼다고 하시네요.
yx는 말 그대로 방향이 나올 수 있는 데이터셋이라고 정의했다고 말씀하셨습니다.
별로 큰 신경은 안 쓰셔도 될 듯 싶습니다. 그냥 단순화를 위한 거예요.
아무튼 손실 함수는 정확히 저 형태가 아닙니다.
mse, rmse 등등 수많은 형태로 응용되어서 사용됩니다.
2.4 경사 하강법의 종류
머신 러닝은 다양한 경사 하강법을 가지고 학습합니다.
잡음이 섞인 데이터, 방대한 매개변수, 일반화 능력이라는 변수들이 있는데, 단순한 경사 하강법으로는 최적해를 찾는 일이 너무나도 어렵고, 시간도 많이 걸립니다.
따라서 머신러닝은 배치 모드 혹은 패턴 모드라는 경사 하강법을 사용합니다.
배치 모드는 틀린 샘플을 모은 다음 한꺼번에 매개변수를 갱신하는 방식이고,
패턴 모드는 패턴 별로 매개 변수를 갱신하는 방식입니다. (세대를 시작할 때 샘플을 뒤섞어 랜덤 샘플링 효과를 제공)
딥러닝은 주로 미니 배치를 사용합니다. (패턴 모드와 배치 모드의 중간)
훈련 집합을 일정한 크기의 부분 집합으로 나눈 다음 부분 집합 별로 처리합니다.
이때 부분 집합으로 나눌 때 랜덤 샘플링을 적용하기 때문에 확률적 경사 하강법(Stochastic gradient descent)이라고도 부릅니다.
3. 요약
아무튼 기본적인 신경망과 퍼셉트론에 대해 알아봤습니다.
추가적으로 학습 방법이 좀 난해하실 수 있는데, 수식을 모두 이해하실 필요는 없고, 그냥 저런 방식으로 하는구나 정도만 아시면 될 것 같습니다.
perceptron : 가장 기본적인 신경망 모델, 여러 개의 입력층과 여러 개의 가중치, 하나의 bias와 하나의 출력노드가 있음
이때 입력 노드와 가중치를 곱해서 모두 더하고 bias 노드를 더한 다음에 활성화 함수에 넣어서 결과 값을 얻음
이때 결과 값과 실제 값이 다를 수도 있는데, 이렇게 되면 가중치를 업데이트 해야함.
이것을 학습이라고 하는데, 학습은 손실 함수(결과 값과 실제 값의 차이)를 줄이는 방향으로 학습함.
이때 어디로, 어느 만큼 가중치를 업데이트해야 하는지에 대한 기법이 경사 하강법임
즉 경사 하강법은 손실 함숫값을 낮추는 방향으로 \(\triangle w\)를 계산함.
감사합니다.
지적 환영합니다.