논문
https://arxiv.org/pdf/1609.05158v2.pdf
0. Abstract
- 최근 몇몇 모델은 복원 전에 bicubic interpolation 등을 사용해서 LR -> HR을 만들었습니다.
- 저자는 해당 방식이 하위 최적화이고, 계산 복잡도를 추가하는 것을 증명할 것입니다.
- 해당 논문에서는 LR 공간에서 뽑아낸 특징 맵을 사용한 CNN 구조를 제안합니다.
- 추가로 마지막 LR 특징 맵에서 HR로 가는 upscaling 필터를 배움으로써 효율적인 sub-pixel conv layer를 소개합니다.
- 성능도 좋았으며, 계산 복잡도도 줄었습니다.
1. Introduction
- SR은 역함수가 없는 low-pass 필터와 subsampling 작업을 통해 손실되는 고주파 정보 때문에 어려운 문제입니다.
- 또한 SR은 LR to HR 매핑은 여러 솔루션을 가질 수 있는 일대다 매핑이고, 올바른 정답을 결정하는 것이 쉽지 않습니다.
- 많은 SR 기술에 놓여져 있는 가정은 고주파의 데이터가 중복적이고, 그러므로 저주파의 구성요소에서 정확하게 복원할 수 있습니다.
- 따라서 SR은 추론 문제이고, 그러므로 이미지의 통계 모델에 의존합니다.
- 많은 방법은 하나의 씬에 다른 관점의 LR을 사용하는데, 이것은 multi-image SR 기법으로 분류될 수 있습니다.
- 추가적인 정보의 downsampling 과정을 뒤집는 시도를 통해 명시적인 중복성을 사용하여 어려운 문제를 해결하려 합니다.
- 다만 해당 방법은 이미지 등록과 혼합(?) 과정을 필요로 하므로 계산 복잡도가 필요합니다.
- affine 변환과 같은 변환에 대한 복잡도인 것 같습니다.
- 대안책으로는 Single Image Super Resolution(SISR)이 있으며, 해당 기법은 함축적인 중복성을 학습하여, LR에서 손실된 HR 정보를 복원합니다.
1.1 Related Work
- 최근 SISR 방법은 edge-based, image statistics based, patch-based 방법이 있다.
- 자세한 방법은 [C.-Y.Yang,C.Ma,andM.-H.Yang.Single-imagesuper-resolution: A benchmark. In European Conference on Computer Vision (ECCV), pages 372–386. Springer, 2014.] 에서 볼 수 있다.
- LR to HR을 복구하기 위해서 희소 사전 학습(sparse dictionary learning) 기법을 사용하는 방식도 있다.
- https://bskyvision.com/entry/%EC%8A%A4%ED%8C%8C%EC%8A%A4-%EC%82%AC%EC%A0%84-%ED%95%99%EC%8A%B5sparse-dictionary-learning%EC%9D%98-%EA%B9%8A%EC%9D%B4-%EC%9E%88%EC%9C%BC%EB%A9%B4%EC%84%9C%EB%8F%84-%EC%89%AC%EC%9A%B4-%EC%9D%B4%ED%95%B4
스파스 사전 학습(sparse dictionary learning)의 깊이 있으면서도 쉬운 이해
오늘은 최근에 논문을 보면서 관심이 생긴 스파스 사전 학습(sparse dictionary learning)에 대해 정리하려고 한다. 스파스 사전 학습은 스파스 코딩(sparse coding)이라는 기법을 활용하는 사전 학습이다.
bskyvision.com
2.1 Motivations and contributions
- SR을 하기 위해서는 LR을 HR 해상도로 올리는 것은 필수적이다.
- 방법 중 하나는 네트워크 중간에서 점진적으로 해상도를 올리거나, 아예 처음부터 해상도를 올리는 것이다.
- 하지만 해당 방법은 많은 단점을 가지고 있는데, 첫 번째로 이미지 퀄리티 향상 작업 전에 해상도를 올리는 것은 계산 복잡도가 올라간다.
- 두 번째는 bicubic 같은 보간 기법을 사용하여 보간하는데, 이 방법은 복원 문제를 해결하기 위한 추가적인 정보를 주지 않는다.
- upscaling을 하는 filter도 있는데, 잘 알려지지 않았고, 구현도 최적화되어있지 않다.
- 따라서 해당 논문에서는 앞선 방법과 다른 방식으로 LR의 특징 맵들로부터 HR을 네트워크의 끝에서 초해상화한다.
- 이를 위해 저자는 sub-pixel convolution layer를 제안한다.
- 이것의 장점은 두 가지이다.
- LR의 공간에서 특징 추출이 이루어지므로, 작은 필터 사이즈가 주어진 정보 공간을 유지하며 같은 정보를 통합할 수 있다. 이는 계산과 공간 복잡도를 확실히 줄일 수 있다.
- L개의 층이 있는 네트워크에서, \(n_{L-1}\) upscaling 필터는 하나의 upscaling 필터가 아닌, \(n_{L-1}\)의 특징 맵에 대한 필터를 학습한다. 명시적인 보간 필터를 사용하는 것이 아닌, 함축적인 정보를 사용한다. 따라서 싱글 필터에 비해 더 좋은 학습을 한다.
2. Method
- \(I^{HR}\) : 원본, rH * rW * C의 텐서를 가진다.
- \(I^{LR}\) : 저해상도, 원본으로부터 가우시안 필터링, r배 다운샘플링을 통해 얻는다. H * W * C의 텐서를 가진다.
- 네트워크 구조는 위와 같다.
- W와 b는 학습이 가능하고, W는 2D conv 텐서이다. 크기는 \(n_{l-1} * n_l * k_l * k_l\)이다.
- n은 필터 개수이며, k는 필터 사이즈이다. \(n_0\)은 C와 같다.
2.1 Deconvoluton layer
- deconvolution은 convolution과 작동 방식은 비슷하지만 이와 반대로 feature map 크기를 증가시킨다.
- 각 픽셀 주위에 zero padding을 추가 후, convolution 연산을 진행한다.
- SRCNN에서 사용된 bicubic interpolation도 이 deconvolution의 특별한 케이스이다.
- 하지만 저자는 다른 방식을 사용합니다.
- 해당 방식을 사용하면 zero padding을 제외한 영역만 정보를 사용할 수 있으므로, 아무래도 성능이 떨어지지 않을까 싶습니다.
2.2 Efficient sub-pixel convolution layer
- 다른 방식은 분할된 1/r의 스트라이드를 사용하는 것이다.
- 그러면 대부분 \((k_s / r) ^ 2\)의 영역만 새롭게 활성화 될 것이다.
- 따라서 (y, x)가 HR의 영역이라면 \(mod(x, r), mod(y, r)\)을 계산하여 HR을 채우면 된다.
- 본 논문에서는 위의 과정에서 \(mod(k_s, r) = 0\)일 때, 아래의 수식을 적용한다.
- 필터 크기인 \(k_s\)가 r의 배수라면, 아래 수식을 적용합니다.
- 만약 필터 크기가 4 * 4이고, r이 4라면 HR에서 채워야 할 공간은 16개의 픽셀이므로, 16개의 특징 맵에서 추출하여 계산합니다.
- (3) 연산은 \(r^2\)개의 특징 맵을 추출하고, PS 연산에 넣습니다.
- (4) 연산은 \(r^2\)개의 픽셀을 각기 다른 채널들에서 추출하여 넣습니다.
- \(W_L = n_{L-1} * r^2C * k_L * k_L\)의 텐서 크기를 가진다.
- 다만 학습을 할 때는 PS 연산을 사용하지 않았습니다.
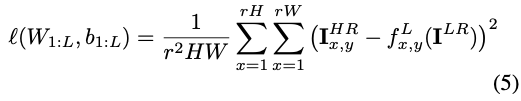
- (5) 연산은 학습에 사용하는 MSE 함수입니다.
- PS 연산을 수행하지 않고, HR의 좌표 (y, x)를 담당하는 \(f^L\)의 특정 채널의 값을 넣은 것으로 보입니다.
3. Experiments
- HR에서 LR을 만들 때는 가우시안 필터, sub-sample을 했습니다.
- 네트워크를 구현할 때는, \(l = 3, \, (f_1, n_1) = (5, 64),\, (f_2, n_2)=(3, 32),\, f_3=3\)입니다. (필터 사이즈, 필터 개수)입니다.
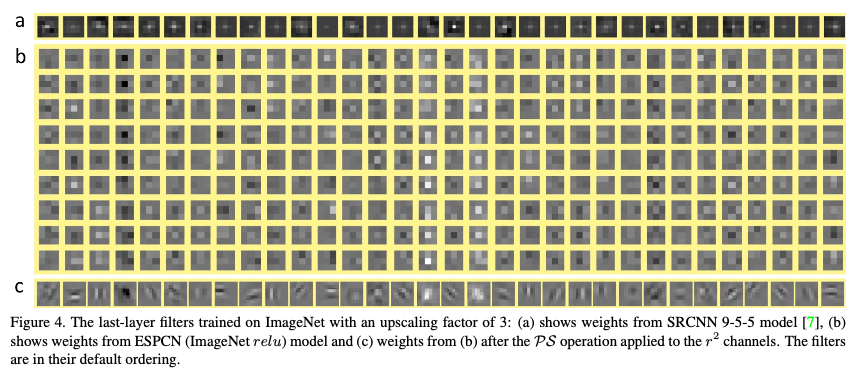
- 특징 맵이 32개이고 이를 9개로 만들어야 하므로, 위와 같은 구조를 가진다.
- r^2 채널에 적용된 PS 연산 후의 b의 모습이 c라고 하는데, 그러면 필터를 대상으로 PS 연산을 해본것인가? 해당 부분은 이해가 잘 안 된다.
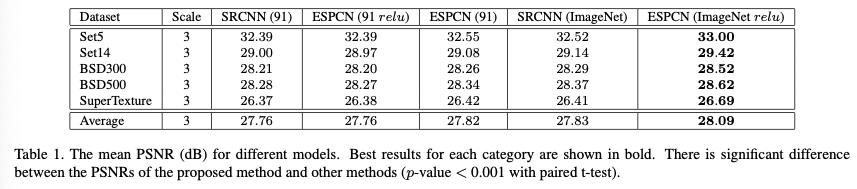
- 구현할 때, relu 대신에 tanh을 사용했다. 위의 표는 relu를 사용했을 때의 비교
- model(91)은 91개의 이미지에 대한 학습 결과이다.
- ESPCN(91)의 경우, tanh이 relu보다 더 학습을 잘했다.
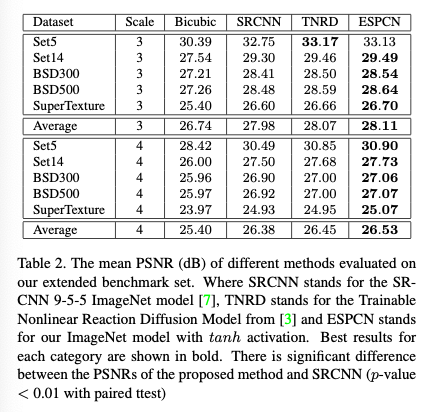
- ESPCN에 대부분 기존의 방법보다 나은 결과를 보인다.
- 이때 사용된 활성화 함수는 tanh이다.
4. Conclusion
- 해당 논문에서는 정적인 업스케일링 기술이 동적인 업스케일링에 비해 안 좋은 결과를 낳고, 더 많은 계산 복잡도를 가짐을 증명했다.
- deconvolution layer와 비교하여 적은 계산 복잡도를 가지며, HR 공간 대신에 LR 공간에서 특징을 추출하는 기법을 사용했다.
- 속도도 빨랐고, 성능도 뛰어났다.
마무리
읽기 쉬운 논문이었다고 생각한다.
이전 기법의 한계에 대해 명확히 설명하고, 제시하는 기법의 장점을 명확히 설명하였다.
하지만 1 ~ 16개의 특징 맵이 순서대로 HR에 부여되는데, 이 순서는 과연 연관성을 가질까? 가 제일 궁금하다.
1번 특징 맵이 (y, x)에 들어간다면 16번 특징 맵은 (y + 3, x + 3)에 들어가는데, 만약 이 두 개의 정보가 매우 다르다면?
또한 1번 특징 맵이 (2 * y, 2 * x)에 들어가면, 16번 특징 맵은 (2 * y + 3, 2 * x + 3)에 들어가야 하는데, 이 두 개의 정보가 매우 흡사하다면?
이런 생각이 꼬리에 꼬리를 물면 하나의 특징 맵에서는 다양한 경우에 대해 학습을 해야 한다.
과연 1번과 16번 특징 맵이 어떻게 학습이 되어야 할지.....
하나의 특징 맵이 각각의 픽셀에 대해서 다르게 학습한다는 것이 매우 어려울 것 같다.