1. Decision Tree (결정 트리)란?
결정 트리는 분류, 회귀 작업도 가능한 강력한 머신러닝 알고리즘입니다.
결정 트리는 if-else문을 사용하여 비교를 하는 간단한 알고리즘이며, 이름에서 알 수 있듯이 Tree와 비슷한 모양을 하고 있습니다.
해당 모델은 Supervised learning method를 사용하고 있으며, 데이터의 특징에서 추론된 간단한 decision 규칙에 의해 예측합니다.
이처럼 결정 트리는 petel length, petal width라는 특징을 이용해 비교를 하고 있으며, 매우 간단합니다.
조건이 True라면 왼쪽으로 이동하고, 조건이 False라면 오른쪽으로 이동합니다.
최종적으로 leaf node에 도착한다면, 해당 노드의 class를 예측 값으로 내는 것이 바로 결정 트리입니다.
특히 결정 트리의 주된 장점은 데이터의 전처리가 필요 없다는 것입니다.
또한 매우 간단하며, 다재다능하고, 모델을 해석(설명 가능)하기 쉽습니다.
2022.05.31 - [Computer Science/머신러닝] - [머신러닝 - 이론] XAI - Explainable AI (설명 가능한 인공지능)
[머신러닝 - 이론] XAI - Explainable AI (설명 가능한 인공지능)
만약 여러분이 카드를 발급받을 때 거부당한다면, 은행 직원에게 이유를 물어볼 수 있습니다. 만약 여러분이 특정 질병을 처방 받는다면, 의사에게 이유를 물어볼 수 있습니다. 이처럼 인간은
hi-guten-tag.tistory.com
특성의 스케일을 맞추거나, 평균을 원점에 맞추는 작업이 필요하지 않습니다.
그렇다면 트리는 어떤 방식을 사용해서 학습을 진행할까요?
2. 학습 방법
결정트리는 노드가 하나도 없는 빈 트리에서 시작합니다.
이때 학습 데이터를 가지고 질문을 가진 루트 노드를 생성합니다.
이때 질문 만들기는 어떤 특징을 사용할지, 해당 특징의 임곗값은 어떻게 할지를 정하는 것입니다.
훈련 집합을 동질성을 가장 잘 확보하도록 부분 집합 2개로 나누는 질문을 찾아내야 합니다.
따라서 특정 노드에 속한 훈련 집합을 최대한 불순도(impurity)가 낮게 분류해야 합니다.
이때 불순도를 측정하는 것이 gini 속성입니다.
\[gini = 1 - \sum_{k = 1}^{n}p_{i, k}^2\]
(\(p_{i, k}\)는 i번째 노드에 있는 훈련 샘플 중 클래스 k에 속한 샘플의 비율입니다. value를 value의 합으로 나눈 것과 같습니다.)
(만약 한 노드의 모든 샘플이 같은 클래스를 가지고 있다면, 이 노드를 순수(gini = 0)하다고 합니다.)
이때 학습은 재귀적으로 이루어집니다.
루트의 왼쪽 자식과 오른쪽 자식을 각각 또다시 루트로 간주하고 같은 과정을 재귀적으로 반복합니다.
해당 이미지는 결정 트리가 만드는 결정 경계를 보여줍니다.
max_depth를 2로 설정했기 때문에 tree는 더 이상 분할되지 않지만, max_depth = 3으로 설정한다면 결정 경계를 추가로 만듭니다.(점선)
결정 트리는 분류뿐만 아니라 확률도 추정할 수 있습니다.
3. 확률 추정
결정 트리는 한 샘플이 특정 클래스 k에 속할 확률도 추정할 수 있습니다.
우선 해당 샘플에 대한 leaf node를 찾기 위해 트리를 탐색하고, 그 노드에 있는 클래스 k의 훈련 샘플의 비율을 반환합니다.
해당 그림에서 petal length = 5, petal width = 1.5인 꽃잎을 발견했다고 가정합시다.
이 샘플에 해당하는 leaf node는 depth = 2의 왼쪽 노드이므로, 해당 노드에서의 클래스 k의 훈련 샘플 비율을 반환합니다.
해당 예시에서는 versicolor일 확률이 49 / 54입니다.
4. CART 훈련 알고리즘
CART는 Classification and Regression Tree의 약자이며, 해당 알고리즘을 사용하여 트리를 훈련합니다.
CART 알고리즘은 훈련 세트를 하나의 특성 k와 임곗값 \(t_k\)를 이용해 두 개의 서브셋으로 나눕니다.
(예를 들면 특성 k <= \(t_k\)를 기준으로)
CART는 (크기에 따른 가중치가 적용된)가장 순수한 서브셋으로 나눌 수 있는 \(k, t_k\)짝을 찾습니다.
해당 알고리즘은 아래와 같습니다.
\[J(k, t_k) = \frac{m_{left}}{m} G_{left} + \frac{m_{right}}{m} G_{right}\]
\(G_{left}, G_{right}\)는 왼쪽/오른쪽의 불순도
\(\frac{m_{left}}{m}, \frac{m_{right}}{m}\)는 왼쪽/오른쪽 서브셋의 샘플 수
따라서 불순도를 최대한 낮추면서, 훈련 샘플을 두 개로 나눕니다.
위에서 말했다시피, 분류에 성공한다면, 같은 방식으로 서브셋을 또 나누면서 재귀적으로 학습합니다.
해당 과정은 설정한 최대 깊이가 되거나, 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 됩니다.
따라서 CART 알고리즘은 Greedy 알고리즘이라 볼 수 있으며, 최적의 솔루션을 보장하지 않습니다.
5. Entropy 불순도
default는 gini 불순도지만, entropy 불순도 또한 사용할 수 있습니다.
분자가 안정되고 질서 정연하면 엔트로피는 0에 가깝습니다.
머신러닝에서는 엔트로피 불순도는 어떤 세트가 한 클래스의 샘플만 담고 있다면 엔트로피가 0입니다.
이때 엔트로피 불순도는 다음과 같습니다.
\[H_i = -\sum_{k = 1}^{n}p_{i, k}log(p_{i, k})\]
만약 \(p_{i, k}\)가 0이라면 H는 0이 된다.
만약 \(p_{i, k}\)가 1이라도 H가 0이 된다.
따라서 불순도를 측정할 수 있다.
그렇다면 지니 불순도와 엔트로피 불순도 둘 중에 무엇이 더 좋을까요?
실제로는 큰 차이가 없습니다.
하지만 지니 불순도는 조금 더 계산이 빠르고, 엔트로피 불순도는 조금 더 균형 잡힌 트리를 만듭니다.
6. 규제 매개변수
결정 트리 같은 모델을 비파라미터 모델(non parameteric model)이라고 합니다.
왜냐하면 결정 트리는 훈련되기 전에는 파라미터 수가 결정되지 않기 때문입니다.
그렇기 때문에 모델 구조가 데이터에 맞춰져서 고정되지 않고 자유롭습니다.
(데이터에 대한 매우 적은 추정만으로도 학습이 가능하다. = 데이터를 몰라도 된다.)
그와 반대로 선형 회귀는 파라미터 모델(parameteric model)이라고 합니다.
이 뜻은 미리 정의된 모델 파라미터를 가지므로 자유도가 제한된다는 뜻입니다.
예를 든다면 Polynomial Regression의 경우 데이터의 input 차원을 미리 가정해야 하고,
Logistic Regression의 경우 이중 분류기로만 쓸 것인지, 다중 분류기로 쓸 것인지 미리 정해야 합니다.
그렇기 때문에 비파라미터 모델은 좀 더 자유롭습니다.
다만, 비파라미터 모델의 단점은 OverFitting이 되기 쉽다는 것입니다.
그대로 가만히 놔둔다면 훈련 데이터에 완전히 밀착되게 학습을 할 것이므로, 이를 제한하기 위해 규제를 해야 합니다.
대표적인 규제는
- restrict Maximum Depth : 트리의 최대 깊이
- min sample split : 분할하기 위한 최소한의 샘플 개수
- min sample leaf : leaf 노드가 가져야 할 최소 샘플 수
- max features : 각 노드에서 분할에 사용할 특성의 최대 수
가 있습니다.
min으로 시작하는 매개변수를 증가시키거나, max로 시작하는 매개변수를 감소시키면 규제가 강해집니다.
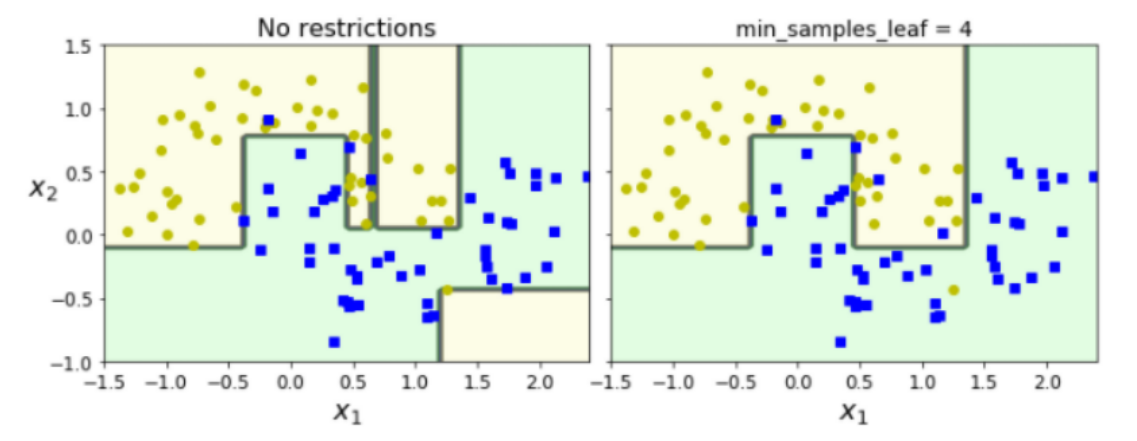
실제로 왼쪽을 보면 약간의 노이즈에도 매우 민감하게 반응하는 모습을 볼 수 있습니다.
오른쪽 모델은 일반화 성능이 더 좋을 것 같아 보입니다.
7. Regression (회귀)
결정 트리의 다재다능함은 회귀까지 가능하다는 것입니다.
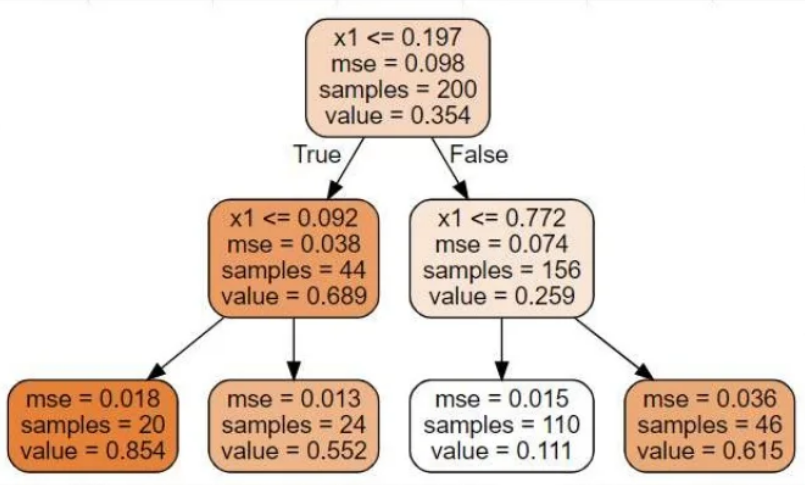
분류 트리와 매우 흡사해 보입니다.
하지만 중요한 차이는 각 노드에서 클래스를 예측(분류)하는 대신 어떤 값을 예측한다는 점입니다.
이때 gini, entropy는 사용할 수 없기 때문에 회귀에 사용되는 MSE를 사용하고 있습니다.
leaf 노드에 도착해서 나오는 value는 해당 노드에 포함되는 샘플의 평균이며, 이때 MSE는 해당 노드에 대한 MSE입니다.
점점 아래로 내려갈수록 MSE가 감소하는 모습을 볼 수 있습니다.
회귀 트리를 결정 경계로 나타내면 아래와 같습니다.
각 영역의 예측 값은 그 영역에 있는 타깃 값의 평균이 됩니다.
알고리즘은 예측값과 가능한 많은 샘플이 가까이 있도록 영역을 분할합니다.
이때 CART 알고리즘도 바꿔야 하는데, 이때의 비용 함수는 아래와 같습니다.
\[J(k, t_k) = \frac{m_{left}}{m} MSE_{left} + \frac{m_{right}}{m} MSE_{right}\]
\(MSE_{node} = \frac{1}{m_{node}}\sum_{i \in node}(\hat{y}_{node}-y^{(i)})^2 \) -> 노드에서의 MSE
\(\hat{y}_{node} = \frac{1}{m_{node}}\sum_{i \in node}y^{(i)}\) -> 노드의 평균
이때도 자유도를 제한하지 않으면 OverFitting이 발생하게 됩니다.
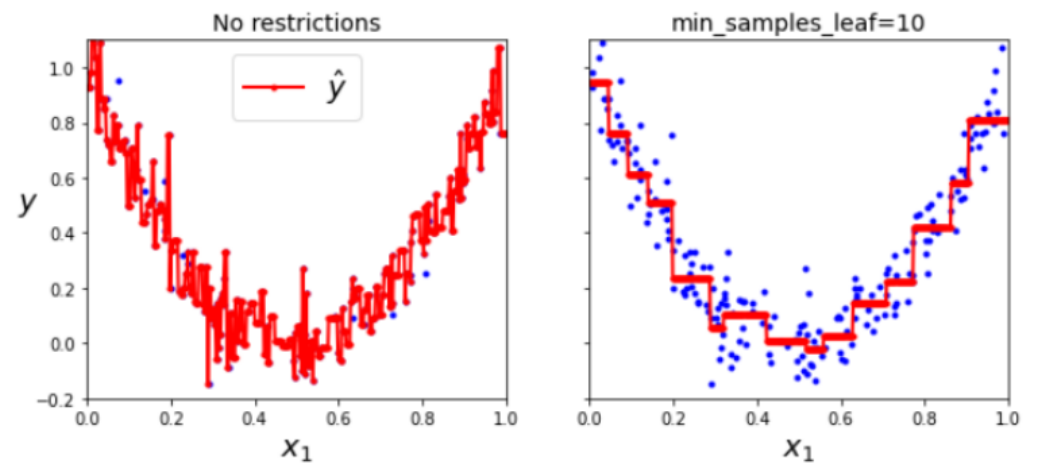
이처럼 Decision Tree는 강력하지만, OverFitting에 매우 취약하다는 단점이 있습니다.
8. Decision Tree의 단점
OverFitting만 해결하면 될 것 같은 Decision Tree도 여러 가지 단점이 있습니다.
첫 번째 단점은 회전에 민감한 점입니다.
결정 트리의 모든 분할은 수직(orthogonal)이므로, 훈련 세트를 약간만 회전해도 이상하게 결정 경계를 만듭니다.
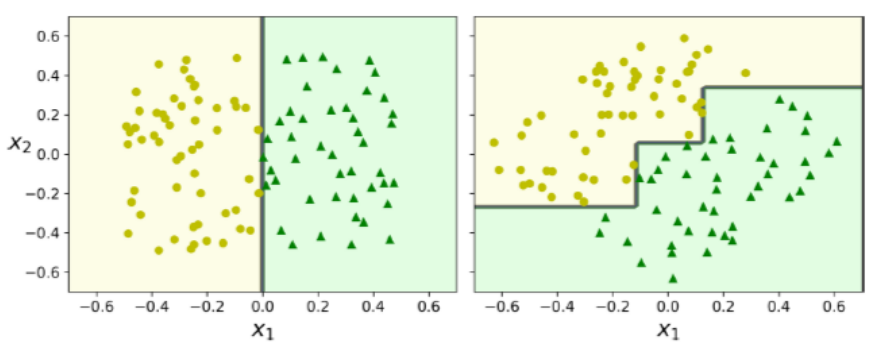
오른쪽 모델이 확실히 일반화가 잘 될 것 같지는 않습니다.
두 번째 단점은 훈련 데이터에 있는 작은 변화에도 매우 민감하다는 것입니다.
훈련 데이터가 약간만 변화되거나, random_state 매개변수를 다르게 설정한다면, 같은 훈련 데이터라도 다른 모델을 얻게 될 수 있습니다.
다음 글에서는 앞선 결정 트리나 다양한 회귀를 조합해서, 더 강력한 모델을 만드는 앙상블 기법에 대해 적도록 하겠습니다.
2022.10.19 - [Computer Science/머신러닝] - [머신러닝 - 이론] Ensemble - Bagging (앙상블 학습 - 배깅)
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] Ensemble - Random Forest (앙상블 학습 - 랜덤 포레스트) (0) | 2022.10.19 |
|---|---|
| [머신러닝 - 이론] Ensemble - Bagging (앙상블 학습 - 배깅) (1) | 2022.10.19 |
| [머신러닝 - 이론] Softmax Regression (소프트맥스 회귀) (0) | 2022.10.18 |
| [머신러닝 - 이론] Logistic Regression (로지스틱 회귀) (0) | 2022.10.18 |
| [머신러닝 - 이론] Regularization (규제) (0) | 2022.10.18 |