인공지능에서의 공간 탐색 능력은 대표적인 예시로 알파고가 있습니다.
현재 게임 상태에서 최적의 다음 상태를 탐색하는 것입니다.
즉 탐색이란 특정 상황에서 최적의 해를 찾기 위해 공간을 탐색하는 것이고,
공간은 문제의 solution이 될 수 있는 집합을 공간으로 가정하는 것입니다.
알고리즘의 BackTracking, Branch and Bound와 흡사하다고 보면 될 것 같습니다.
최적의 해를 찾기 위해 solution 혹은 경우의 수들을 공간으로 가정하고, 그 공간을 탐색하는 것이 탐색, search입니다.
예를 들면 어떻게 골을 넣을 수 있을까, 다음 수를 어떻게 둬야 게임에서 이길 수 있을까와 같이 특정한 목표를 가지고 탐색하는 것이라고 보면 되겠습니다.
이때 상태 공간(State Space)에 대해 이해할 필요가 있습니다.
1. 상태 공간 (State Space)
상태 공간은 발생할 수 있는 모든 상태를 포함하는 집합입니다.
모든 경우의 수를 포함하고 있다고 보면 됩니다.
예를 들어 8-퍼즐의 경우 9! 크기의 상태 공간을 가지고 있습니다.
스도쿠는 훨씬 큰 상태 공간을 가지고 있습니다.
State Space Tree란 상태들이 서로 연결되어 있어 트리 형태로 그린 것입니다.
이때 목표하는 상태를 효율적으로 찾는 지능적인 공간 탐색 알고리즘을 생각해야 합니다. (DFS, BFS, Best FIrst Search)
제가 작성한 알고리즘의 글에서 BackTracking과 Branch and Bound를 생각하시면 될 것 같습니다.
요약하자면 상태들이 서로 트리 형태로 연결되어 있고, 이러한 트리를 효율적으로 탐색해서 최적의 해를 찾는 것이 바로 인공지능 탐색의 목표입니다.
이제 공간을 탐색하는 알고리즘을 소개하겠습니다.
2. 상태 공간 탐색 알고리즘 (State Space Search Algorithm) - 맹목적 탐색
맹목 탐색은 어떠한 정보, 효율적인 전략 없이 주어진 순서대로 탐색하는 알고리즘입니다.
BFS와 DFS가 있습니다.
이때 BFS는 항상 최적해를 보장합니다.
모든 깊이에서 가능한 모든 자식 노드를 살피기 때문입니다.
하지만 너무 많은 대안을 살펴서 매우 느리다는 단점이 있습니다. 따라서 전략적으로 해를 찾는 보다 똑똑한 알고리즘이 필요합니다.
참고로 DFS는 속도는 조금 더 빠를 수 있어도 최적해를 보장하지 않습니다.
왜냐면 무한 루프에 빠질 가능성이 있고, 무한 루프를 돌면 다른 최적화된 루트를 볼 수 없기 때문입니다.
3. 상태 공간 탐색 알고리즘 (State Space Search Algorithm) - 휴리스틱 탐색
네이버 지식백과에서는 휴리스틱을 다음과 같이 설명하고 있습니다.
시간이나 정보가 불충분하여 합리적인 판단을 할 수 없거나, 굳이 체계적이고 합리적인 판단을 할 필요가 없는 상황에서 신속하게 사용하는 어림짐작의 기술
똑똑한 알고리즘을 위해서 문제의 특성을 이용해야 합니다.
blind search의 비효율성은 주어진 문제의 특성을 이용하지 않기 때문입니다.
이때 문제의 특성을 이용하는 방식을 경험적 탐색, 휴리스틱 탐색 (heuristic function)이라고 합니다.
이러한 휴리스틱 탐색의 종류는 best-first-search, a* search 등이 있습니다.
이때 상태의 좋은 정도를 측정하는 평가 함수(evaluation function)으로 휴리스틱 함수(heuristic function)이 있습니다.
다양한 함수 방법이 있지만, 8-퍼즐의 경우 "위치와 불일치 하는 수를 세는 함수"와 "제자리를 찾아가는데 필요한 거리의 합을 세는 맨해튼 거리의 합 함수"가 있습니다.
가장 좋은 상태의 자식 노드를 먼저 방문하기 위해서는 Priority Queue가 필수적입니다.
3.1 Best-First-Search
Best First Search의 경우 자식을 평가한 후 가장 좋은 자식을 먼저 방문하는 탐색 방법입니다.
이때 목표하는 지점까지 가장 가까운 노드를 우선적으로 확장하여 탐색합니다.
하지만 이때 목표하는 지점까지의 정확한 거리가 얼만큼 되는지를 몰라서 예상치를 추정하여 탐색합니다.
3.2 A* Algorithm
A* 알고리즘은 최고 우선 탐색의 한계를 개선하기 위해 만들었습니다.
최고 우선 탐색의 경우 트리를 타고 내려온 이전의 기록들은 무시한 채 현재 상황에서 어떤 경로로 트리를 타고 내려가야 가장 유리할지를 결정합니다.
현재 노드까지 오는데 걸린 비용은 생각하지 않고, 당장 앞으로 어디를 가야할지를 결정하는 방법입니다.
A*는 남은 경로의 길이와 지금까지 온 경로도 고려하자라는 알고리즘입니다.
이때 A*가 사용하는 휴리스틱 함수를 보면,
f(s) = g(s) + h(s)가 있습니다. g(s)는 현재 상태 s까지 찾아 오는데 사용한 비용이고, h(s)는 목표하는 상태를 찾아가는데 필요한 비용의 추정치입니다.
4. 상태 공간 탐색 알고리즘 (State Space Search Algorithm) - 게임 트리
지금까지는 혼자 하는 게임을 대상으로 했지만, 게임 트리에서는 두 사람이 번갈아 수를 두고 승패를 겨루는 게임으로 생각합니다.
체스, 바둑 등에 사용되고, 상대가 어떻게 하느냐에 따라서 방법이 완전히 달라지므로 경우의 수가 너무나도 많습니다.
게임의 결과는 마지막에 볼 수 있고, 최대한 많은 수를 보는게 유리합니다.
4.1 Mini-Max Algorith
mini max 알고리즘은 트리로 이루어져 있습니다.
이때 두 명의 플레이어가 게임을 하므로, 자신이 택할 수 있는 모든 경우의 수를 트리로 구현합니다.
상대가 어떤 수를 둘지 모르는데 어떻게 최적의 선택을 하는지 궁금한데, 미니맥스에서는 상대방도 최적의 수를 선택한다고 가정합니다.
미니맥스 전략은 내가 둘 차례에는 max를 선택하고, 상대 차례에서는 min을 선택합니다.
상대의 최적의 수는 나에게 최악의 수기 때문입니다.
우선 모든 Tree를 만들고 리프 노드에서 휴리스틱 함수를 통해 가치를 평가합니다.
이때 min max 전략이 나옵니다.
만약 리프 노드(n)가 내 차례였다고 했을 때, 리프 노드의 바로 위 노드(n - 1)는 상대방의 차례가 됩니다.
따라서 바로 n - 1노드에서는 n 노드들 중에 가장 작은 값을 선택합니다.
그리고 n - 2 노드에서는 n - 1 노드들 중 가장 큰 값을 선택합니다.
이러한 방식으로 최상위 노드를 갔을 때, 나오는 값이 내가 다음에 수행해야 하는 경우의 수입니다.
하지만 미니 맥스 또한 너비 우선 탐색을 한다고 볼 수 있습니다.
틱택톡의 게임에서는 바닥 깊이인 9까지 내려가면 경우의 수가 8!개나 있습니다.
만약 체스, 바둑의 경우에는 얼마나 많을까요?
따라서 이런 비효율적인 문제를 해결해야만 합니다.
인공지능은 감당할 수 있는 정도까지만 내려가서 승패가 결정되지 않은 상태에 휴리스틱 함수를 적용합니다.
4.2 alpha-beta pruning Algorithm
알파베타 가지치기 알고리즘은 DFS를 이용해서 탐색합니다.
이때 제한 깊이까지만 탐색합니다.
즉 일정 수준의 깊이까지만 내려갔다가 거기서 멈추고, 그 상태에서 휴리스틱 함수를 통해 가치를 평가합니다.
혹은 내려가는 와중에 개선의 가능성이 없는 노드는 탐색하지 않습니다.
alpha 가지치기는 min에서 가지치기를 합니다.
beta 가지치기는 max에서 가지치기를 합니다.
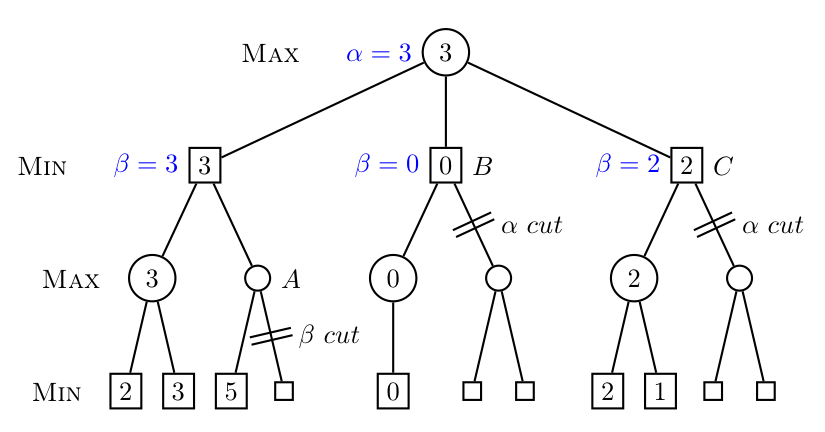
왼쪽부터 beta, alpha, alpha 가지치기가 있습니다.
이때 맨 왼쪽의 가지치기를 먼저 보겠습니다.
만약에 A의 값이 5 이상의 값이 된다면, 그 위의 부모 노드는 3을 선택할 것입니다.
만약 A의 자식 노드의 오른쪽 값이 5 이하의 값이 된다면 A는 필연적으로 5가 됩니다.
따라서 beta 가지치기를 통해 아래의 자식 노드는 탐색하지 않습니다.
맨 오른쪽의 alpha 가지치기를 보면, C가 2 이하의 값이 된다고 하더라도, 최상단 노드에서는 3을 선택할 것이 뻔하기 때문입니다.
마찬가지로 2 이상의 값은 될 수 없기 때문에 alpha 가지치기를 통해 자식 노드를 탐색하지 않습니다.
즉, 내가 선택하지 않거나, 상대방이 선택하지 않을게 뻔하기 때문에 가지치기를 하는 것이 alpha-beta pruning입니다.
하지만 이러한 방식 또한 효율을 높여주는 주지만 과다한 계산 시간은 여전합니다.
여전히 BFS를 하긴 해야하고, 알파 베타 가지치기가 완벽하게 복잡도를 줄여주지는 않습니다.
따라서 이제는 휴리스틱 함수가 없이 동작하는 탐색 알고리즘을 구현해야 합니다.
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] XAI - Explainable AI (설명 가능한 인공지능) (0) | 2022.05.31 |
|---|---|
| [머신러닝 - 이론] MCTS (Monte Carlo Tree Search) (몬테카를로 트리 탐색) (0) | 2022.05.29 |
| [머신러닝 - 이론] GAN (Generative Adversarial Network) (생성적 적대 신경망) (0) | 2022.05.29 |
| [머신러닝 - 이론] Generative Model (생성 모델) (0) | 2022.05.29 |
| [머신러닝 - Python] 손실함수 - 오차제곱합, 교차엔트로피 합 구현 (Loss Function - Sum of Squares Error, Cross Entropy Error Implementation) (0) | 2022.05.09 |