앞선 글에서는 딥러닝이 무엇인지, 손실 함수는 어떻게 정의되고, 가중치 갱신 규칙에 대해 간략하게 알아봤습니다.
딥러닝의 학습 알고리즘은 수학적으로 아주 깔끔합니다.
하지만 층이 깊어질수록 딥러닝의 학습 중 발생하는 현실적인 문제를 말하고, 해결 전략에 대해 설명해드리겠습니다.
그리고 뒤에서는 몇몇 중요한 손실 함수와 옵티마이저 함수의 종류에 대해서 설명하겠습니다.
마지막으로 하이퍼 파라미터의 최적화 방법에 대해 알려드리겠습니다.
대표적인 두가지 문제는 그레이디언트 소멸 문제(Vanishing Gradient Problem), 과잉 적합 문제(Over Fitting Problem)입니다.
1. 그레이디언트 소멸 문제 (Vanishing Gradient Problem)
가중치를 갱신하는 과정은 미분의 연쇄 법칙을 따릅니다.
이때 I번째 층의 그레이디언트는 오른쪽에 있는 I+1번째 층의 그레이디언트에 자신 층에서 발생한 그레이디언트를 곱하여 구합니다.
쉽게 말해서 출력 층에서 입력 층으로 오차가 전달되면서, 은닉 층의 가중치가 갱신되는데, 이때 오차가 점점 사라지면서 입력 층에 가까운 은닉 층은 갱신이 되지 않는 문제가 발생합니다.
대충 이렇게만 이해하셔도 괜찮은데, 정말 제대로 된 수식이 알고 싶으신 분들은
(참고로 모두 수학입니다만, 이론적인 배경을 알기엔 정말 좋은 블로그라고 생각합니다.)
오차 역전파(error backpropagation) 개념 제대로 파악하기
미리 말씀드리지만 이 글은 좀 깁니다. 그리고 수식이 많아서 언뜻 보면 너무 어렵게 느껴질 수 있습니다. 하지만 이 글을 끝까지 인내하시면서 읽어내려가신다면 분명 오차 역전파(error backpropag
bskyvision.com
이 분의 오차 역전파에 대해 설명하신 것을 보시면 됩니다.
그러면 가중치 갱신이 우측에서 좌측으로 가면서 미분을 통해 이루어진다는 사실을 알 수 있으실 겁니다.
1.1 그레이디언트 소멸 문제의 해결책
우측에서 좌측으로 갈수록 미분 값이 점점 줄어들다가 소멸되는 문제입니다.
이때 해결책은 과연 뭘까요?
바로 미분 값을 안 줄어들게 하면 됩니다.
이때 나온 손실 함수가 ReLU 함수입니다.

ReLU함수는 이렇게 생겼죠?
Tanh(s) 시그모이드 함수는 이렇게 생겼습니다.

두 개의 차이점이 보이시나요?
ReLU 함수는 s가 음수일 때는 그레이디언트가 0, 양수일 때는 1로 동일하지만,
Tanh(s) 함수는 s가 클 때 그레이디언트가 0에 가까워집니다.
손실 함수를 ReLU로 사용함으로써 그레이디언트 소멸 문제를 방지합니다.

한 번 수식으로 표현해봤습니다.
음....
이제 보니까 학습률 안에 -를 곱한다는 걸 깜빡했군요..
아무튼 중요한건 저기 뒤에 \(\frac{\partial a(W X^T)}{\partial W}\) 라는 식이 있는데,
이때 a가 활성화 함수입니다.
왜 그레이디언트 소멸 문제에서 활성화 함수의 미분 값이 중요한지 아시겠죠?
2. 과잉 적합 (Over Fitting)
과잉 적합이란 모델이 훈련 데이터에 대해 너무나도 과도하게 적합한 학습을 한 현상입니다.
이때 Over Fitting을 피할 수 있는 방법은
- 데이터 양을 늘림
- 만약 데이터의 양을 늘릴 수 없다면, 훈련 샘플을 인위적으로 변형하여 데이터를 증대 (data augmentation)합니다.
- 규제 기법 적용
- 데이터 증대, 가중치 감쇠, 드롭아웃, 앙상블
- 추후에 설명합니다.
3. 딥러닝이 사용하는 손실 함수
평균 제곱 오차(MSE : Mean Squared Error)는 다음과 같습니다.
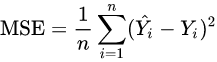
이때 보시면 값을 제곱하기 때문에 1미만의 값은 작아지고, 1 이상의 값은 커집니다.
따라서 학습이 느려지거나, 학습이 안 되는 상황을 초래할 가능성이 있습니다.
또한 제곱하기 때문에 특이값의 영향을 더 크게 받습니다.
회귀를 위해 사용하는 손실 함수에는 MSE, MAE, RMSE 등이 있고,
분류를 위해 사용하는 손실 함수에는 Binary-Cross Entropy, Categorical-Cross Entropy등이 있습니다.
아무튼 분류를 위해서는 위의 MSE와 같은 손실 함수를 사용하면 안 되고, 엔트로피 함수를 사용해야 합니다.
3.1 엔트로피 (entropy)
엔트로피는 확률 분포의 무작위성(불확실성)을 측정하는 함수입니다.
공정한 주사위의 엔트로피는 찌그러진 주사위보다 높습니다.
왜냐면 찌그러진 주사위는 불확실성이 낮기 때문이죠
이때 엔트로피를 교차하여 두 개의 확률 분포가 다른 정도를 측정하는 함수를 교차 엔트로피 (cross entropy)라고 합니다.
3.2 교차 엔트로피 (cross entropy)
교차 엔트로피의 공식은
\(H(P,Q) =-\sum_{i=1,k}P(e_i)logQ(e_i)\)
입니다.
예를 들어 공정한 주사위 P와 Q의 교차 엔트로피는
\(-(\frac{1}{6}\log \frac{1}{6} + \cdots +\frac{1}{6}\log \frac{1}{6}) = 1.7918\)이고,
공정한 주사위 P와 찌그러진 주사위 Q(1이 1/2, 나머지는 1/10의 확률)의 교차 엔트로피는
\(-(\frac{1}{6}\log \frac{1}{2} + \frac{1}{6}\log \frac{1}{10}+\cdots +\frac{1}{6}\log \frac{1}{10}) = 2.0343\)입니다.
즉 교차 엔트로피의 값이 클수록 정보량(에러)이 더 많습니다.
교차 엔트로피는 MSE의 불공정성 문제를 해결해줍니다.
즉 교차 엔트로피 손실 함수 : \(e=-\sum_{i=i,c}y_i\log o_i\)이 됩니다.
4. 딥러닝이 사용하는 옵티마이저
옵티마이저는 손실 함수를 적게 만드는 기법입니다. 말 그대로 최적화하는 기법입니다.
앞선 글에서 저희는 옵티마이저 기법에 대해 경사 하강법과 SGD(Stochastic Gradient Descent) 옵티마이저에 대해 알아봤습니다.
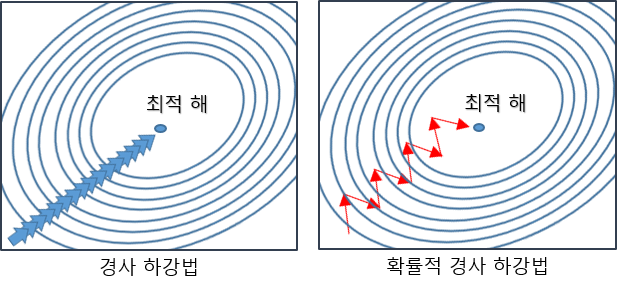
다시 설명드리자면 경사 하강법은 모든 데이터에 대해 최적화를 수행합니다.
하지만 확률적 경사 하강법은 데이터를 배치 사이즈로 나누어 배치 사이즈 별로 최적화를 수행합니다.
이때 표준에 해당하는 SGD 옵티마이저를 개선하는 두 가지 아이디어가 있는데, 이걸 설명해드리겠습니다.
4.1 모멘텀(momentum)을 적용한 옵티마이저
물리에서의 모멘텀은 이전 운동량을 현재에 반영하는 것입니다. 즉, 관성과 관련이 있습니다.
옵티마이저에 모멘텀을 적용하면 뚜렷한 성능의 향상이 보입니다.
만약에 SGD 옵티마이저를 사용한다면, 가중치 해가 심하게 지그재그 하거나, local minimum에 위치할 수도 있습니다.
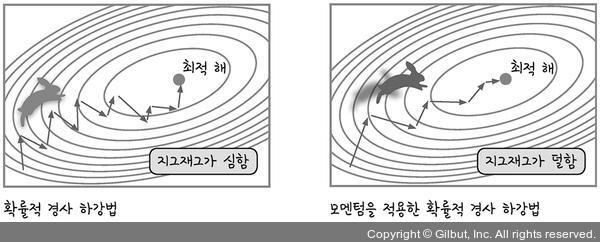
위 그림처럼 고전적 SGD에 모멘텀을 적용하면 관성이 부여되어 가고자 하는 방향으로 좀 더 나아갑니다.
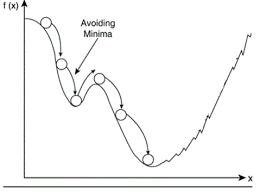
또한 고전적 SGD는 local minimum에 위치할 수도 있습니다. 이때 SGD는 이 점이 global minimum이라고 생각하여 여기가 최적의 해라고 도출할 수도 있습니다.
하지만 우리는 local minimum이 global minimum이 아닌 걸 알 수 있습니다.
이때 모멘텀을 적용하면 관성이 생겨서 local minimum을 쉽게 탈출할 수 있습니다.
모멘텀은 이전 방향 정보 v를 같이 고려합니다.
수식으로 표현하면
고전적 SGD : \(w=w-\rho\frac{\partial J}{\partial w}\)
모멘텀을 적용한 SGD :
\(v = \alpha v - \rho\frac{\partial J}{\partial w}\)
\(w = w + v\)
입니다.
\(\alpha\)는 0~1 사이에서 조절하는데, \(\alpha = 0\)이면 고전적 SGD이고, \(\alpha\)가 1에 가까울수록 이전 정보에 큰 가중치를 부여합니다.
추가로 네스테로프 모멘텀이라는 모멘텀을 조금 변형한 옵티마이저도 있습니다.
현재 점 w에서 미분하는 대신, 이전 정보인 \(\alpha v\)를 이용하여 다음에 이동할 곳 \(\hat{w}\)를 예측하고, 그곳에서 그레이디언트를 계산하는 방식입니다.
기존의 모멘텀은 멈춰야 할 곳을 넘어서 멈출 수 있는데, 네스테로프 모멘텀을 적용하면 중간에 멈춰서 계산해서 다시 가기 때문에 적절한 시점에 제동을 겁니다.
4.2 적응적 학습률 (learning rate scheduler)을 적용한 옵티마이저
그레이디언트는 최저점의 방향을 알려주지만 이동량에 대한 정보가 없기 때문에 저희는 앞에 \(\rho\)를 곱해서 이동합니다.
이때 작은 학습률을 곱해 조금씩 보수적으로 이동합니다.
학습률이 너무 작으면 학습에 많은 시간이 소요되고, 학습률이 너무 크면 진동할 가능성이 있습니다.
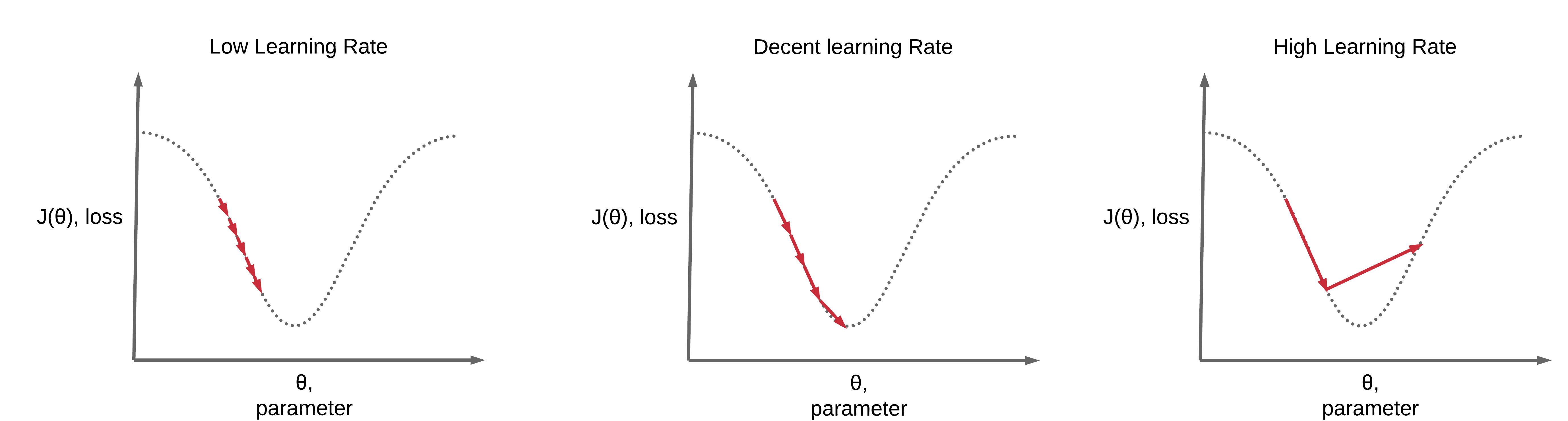
위의 그림과 같이 진동하거나, 많은 시간을 쓰지 않기 위해서 저희는 learning rate scheduler를 적용합니다.
쉽게 말해서 멀리 있으면 학습률을 높이고, 가까이 가면 학습률을 줄이는 방식입니다.
적응적 학습률에 대한 기법으로는
- Adagrad : 이전 그레이디언트를 누적한 정보를 이용하여 학습률을 적응적으로 설정하는 기법
- RMSprop : 이전 그레이디언트를 누적할 때 오래된 것의 영향을 줄이는 정책을 사용하여 Adagrad를 개선한 기법
- Adam : RMSProp에 모멘텀을 적용하여 RMSprp를 개선한 기법
대다수의 딥러닝은 Adam을 사용합니다.
왜냐면 모멘텀과 적응적 학습률을 모두 적용했기 때문입니다.
Adam이 좋아요
5. 교차 검증(cross validation)을 이용한 하이퍼 매개변수 최적화 (Hyper Parameter Optimizer)
매우 중요한 파트입니다.
교차 검증은 우연을 배제하는데 매우 효과적입니다. 우연히 훈련 세트나 테스트 세트를 잘 맞추는 모델이 있을 수도 있기 때문에, 교차 검증을 통해서 우연을 배제합니다.
하지만 교차 검증은 시간이 오래 걸린다는 단점이 있습니다.
하지만 그래도 신뢰도를 높인다면 그만한 장점이 없겠죠??
하이퍼 파라미터(Hyper parameter)는 모델을 만들 때, 인간이 일일이 설정해줘야 하는 값입니다.
모델이 어떤 손실 함수를 사용할지, 어떤 활성화 함수를 사용할지, 어떤 옵티마이저를 사용할지, 몇 개의 은닉층, 은닉층의 노드 개수 등등 수많은 하이퍼 파라미터가 있습니다.
심지어 한 개의 하이퍼 파라미터라 하더라도 안에 적용할 수 있는 파라미터는 더 많죠.
아무튼 이런 하이퍼 파라미터들을 비교하기 위해서 교차 검증을 이용합니다.
제가 곰곰이 생각해보니까 최적의 하이퍼 파라미터를 구하는 방법을 말을 안 했네요...
다음 글에 바로 써야겠네요.
아무튼 교차 검증을 통해서 어떤 하이퍼 파라미터가 가장 좋은 결과를 내는지를 보고 결정하시면 됩니다.
참 귀찮죠?
전 모델 하나 교차 검증하는데 1시간이나 걸린 적이 있습니다.....
6. 요약
딥러닝의 문제점은 그레이디언트 소멸 문제, 과잉 적합 문제 등이 있습니다.
그레이디언트 소멸 문제를 해결하기 위해서는 활성화 함수를 다른 활성화 함수로 바꾸는 방법이 있습니다.
ex) ReLU
또한 과잉 적합 문제를 해결하기 위해서는 데이터 셋을 증가, 규제, 드롭아웃, 앙상블 등의 방법이 있습니다.
이때 데이터 셋을 증가할 수 없다면 인위적으로 증가시키는 법을 data augmentation이라고 합니다.
또한 딥러닝이 사용하는 다양한 손실 함수에 대해서도 알아봤는데요.
대표적으로 MSE와 cross-entropy가 있습니다.
MSE는 회귀(ex. 집값이 얼마냐?)에 사용되고, 만약에 분류나 확률에 사용한다면 MSE는 1보다 낮은 값에 대해서는 작아지고, 1보다 큰 값에 대해서는 커지기 때문에 불공정합니다.
따라서 분류나 확률에 대해서는 cross-entropy 손실 함수를 사용합니다.
cross-entropy는 분류나 확률의 분포에 대해서 두 개(예측 값, 타겟 값)를 비교합니다.
cross-entropy가 클수록 두 개의 차이가 크다는 것을 의미합니다.
이런 손실 함수의 최저점을 찾기 위한 기법인 옵티마이저에 대해서도 알아봤습니다.
기존의 SGD 옵티마이저는 지역 최저점에 갇히거나, 학습률이 작으면 너무 느리고, 학습률이 크면 지그재그가 심한 현상이 있었습니다.
이때 지역 최저점이나 지그재그를 막기 위해서 모멘텀을 적용할 수가 있고,
학습률의 변화를 위해서 다양한 기법을 적용할 수 있습니다.
대표적으로 RMSprop 기법, adam 기법이 있습니다.
마지막으로 교차 검증을 이용한 하이퍼 파라미터 최적화가 있는데, 단순히 교차 검증을 통해 신뢰도를 올리고, 이런 신뢰를 바탕으로 다양한 하이퍼 파라미터를 검사해서 최적의 파라미터를 찾아내는 과정입니다.
다음 글에서는 하이퍼 파라미터를 찾는 Grid Search, Randomized Search에 대해서 알아보겠습니다.
감사합니다.
지적 환영합니다.