앞의 글을 읽으시면 이해에 도움이 됩니다.
2022.11.22 - [Computer Science/컴퓨터 구조] - [컴퓨터 구조] The Basic of Cache
[컴퓨터 구조] The Basic of Cache
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.11.22 - [Computer Science/컴퓨터 구조] - [컴퓨터 구조] Introduction to the Memory Hierarchy [컴퓨터 구조] Introduction to the Memory Hierarchy 앞의 글을 읽으시면 이해
hi-guten-tag.tistory.com
1. Direct Mapping
Direct mapping 기법은 cache와 memory를 mapping하는 가장 간단한 방법입니다.
memory 주소에 따라 cache에 넣을 수 있는 공간을 제한합니다.
이는 1:1 대응 관계에 있으며, 특정 memory 주소는 특정 cache의 block에만 들어갈 수 있습니다.
그림으로 한 번 봅시다.

Cache의 block size는 8이므로, Memory를 8개로 나누어서 각각 mapping 합니다.
이때 1:1 대응 관계에 있으므로, 만약 memory 주소 00001이 cache의 001에 이미 위치하고 있다면,
다른 메모리 정보가 들어가기 위해서는 교체를 해야 합니다.
2. Mapping 방식
mapping의 방식은 메모리 주소의 하위 비트를 사용하는 것입니다.
00001, 01001, 10001, 11001의 공통점은 하위 3비트가 모두 001로 끝난다는 점입니다.
그렇기 때문에 cache의 001 block으로 mapping 됩니다.
따라서 필연적으로 cache는 2의 거듭제곱의 block 개수를 가져야 합니다.
(만약 cache의 size가 16이라면 하위 4개의 비트를 사용함)
이때 mapping 위치에 대한 계산은 아래와 같습니다.

01101은 13 % 8 = 5이므로, cache의 5번째 block에 mapping 됩니다.
이처럼 간단하게 mapping을 할 수 있지만, 두 개의 단점이 있습니다.
첫 번째는 빈 공간이 있다 입니다. 만약 끝자리가 001로 끝나는 메모리 주소만 사용한다면 어떻게 될까요?
cache의 남은 7개의 공간은 사용하지 않고, 빈 공간이 되므로 비효율적입니다.
이는 Associative Mapping에서 해결합니다.
두 번째는데이터가 쓰레기인지 아닌지, 또한 메모리의 어떤 주소에서 온 건지에 대한 정보도 알고 있어야 한다 입니다.
만약 Processor가 11001에 대한 데이터를 요청했다고 가정해봅시다.
cache를 처음 초기화할 때는 쓰레기 값이 들어갑니다.
만약 cache가 memory와 mapping 되지 않았다면, 쓰레기 값이 계속 존재합니다.
따라서 cache의 001번지의 값이 쓰레기인지 아니면 원하는 데이터인지 알 수 없습니다.
만약 쓰레기 값이 아니라면 어떻게 될까요?
cache의 001번지에 가서 데이터가 존재한다는 것을 알았는데, 이것이 11001인지, 00001인지, 아니면 다른 어떤 XX001인지 알 수 없습니다.
따라서 cache는 본인의 block에 있는
데이터가 쓰레기인지 아닌지, 또한 메모리의 어떤 주소에서 온 건지에 대한 정보도 알고 있어야 합니다.
3. Tags and Valid Bits
cache는 데이터의 유효성 함께 어느 메모리 주소에서 데이터가 왔는지도 알아야 합니다.
이를 해결하는 것이 바로 Tags와 Valid Bits입니다.
우선 Tag부터 봅시다.
각 cache의 위치는 여러 다른 메모리 주소의 정보를 포함할 수 있습니다.
이때 하위 비트는 cache의 번지로 지정되어 있으므로, 메모리 주소를 지정하기 위해서는 상위 비트가 추가적으로 필요합니다.
이때 상위 비트를 tag라고 부릅니다.
11001에서 하위 비트는 001, 상위 비트(tag)는 11이 됩니다.
따라서 cache는 tag 정보도 함께 저장합니다.
구조는 아래와 같습니다.

index와 offset은 뒤에서 설명합니다.
다음은 valid입니다.
valid bit는 의미 없는 데이터와 tag를 구별하기 위해 추가되었습니다.
초기화를 할 때, 각 cache의 위치한 valid bit는 0이 되며, 이는 곧 해당 cache의 값이 쓰레기임을 의미합니다.
반대로 valid bit가 1이라면, 해당 cache의 값이 유효합니다.

tag와 valid가 어떻게 변하는지 한 번 예시를 봅시다.
4. Accessing a Cache

위의 순서대로 processor가 참조한다고 가정해봅시다.

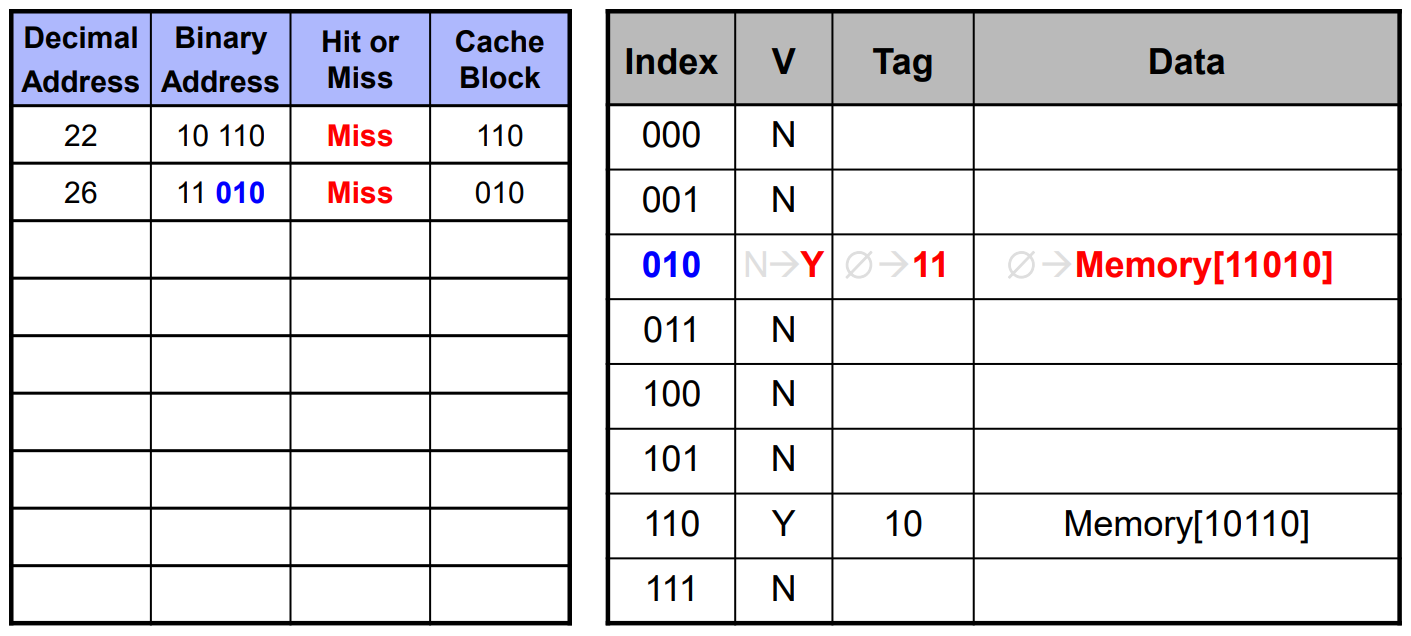
10 110, 11 010 둘 다 cache의 mapping 위치의 valid bit가 0이므로, miss입니다.

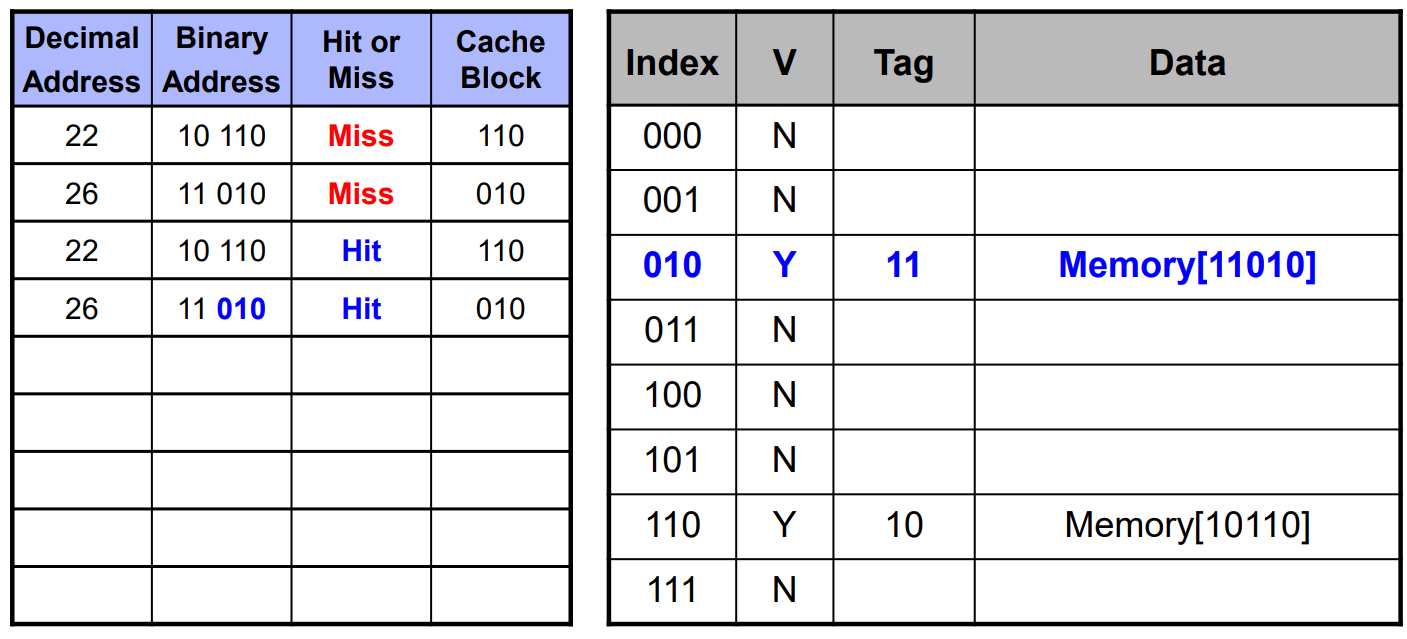
여기서 Valid = Y라고 무작정 가져오면 안 되고, tag field도 같은지 확인해야 합니다.
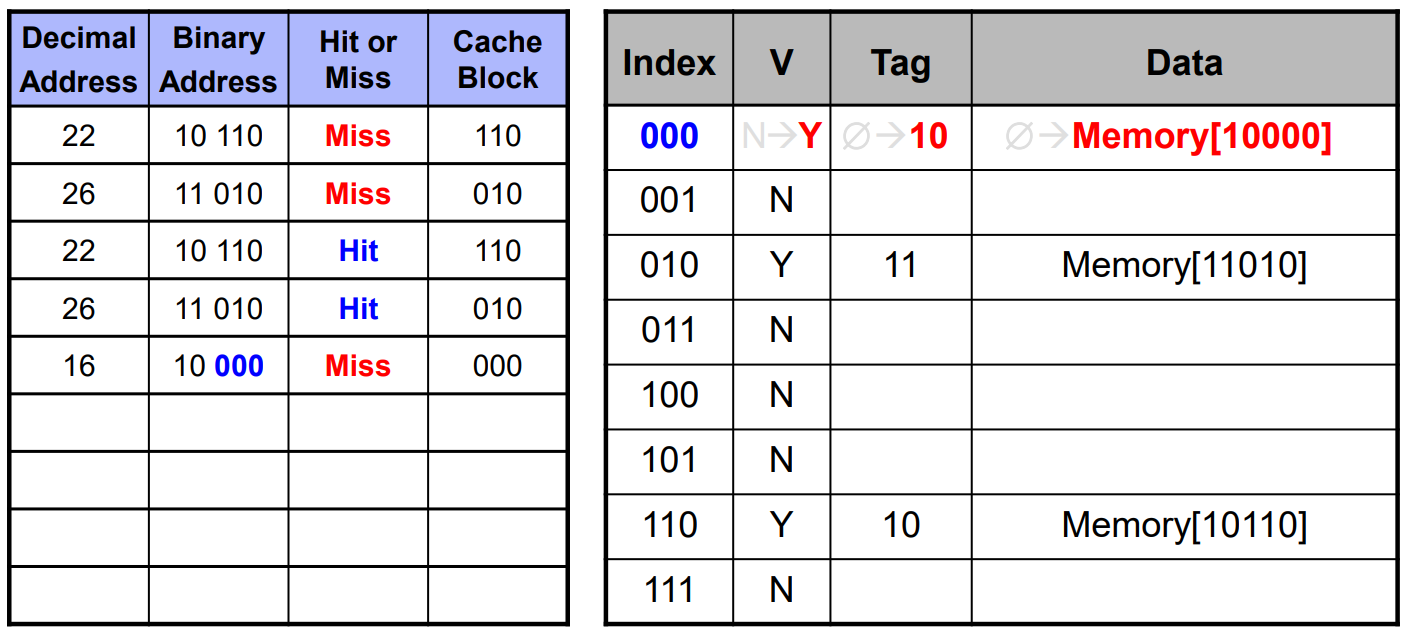
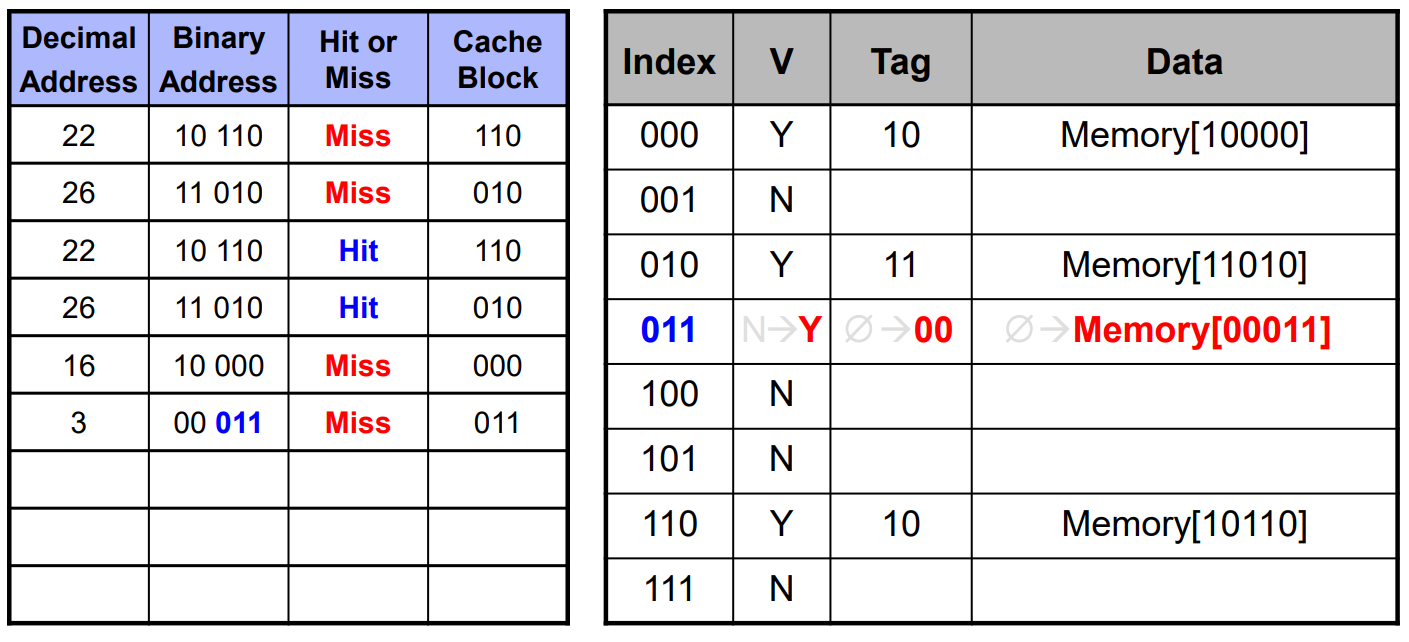


우측을 보면 10 010을 가져오는데, cache의 010을 보면 valid bit가 Y입니다.
그러나 tag field가 다르기 때문에 Miss입니다.

꽤.. 많네요...
마지막으로 cache를 참조하기 위한 참조 주소를 알아봅시다.
5. Reference address
Reference address는 총 3개로 나눌 수 있습니다.
tag field, cache index, byte offset입니다.
- tag field : cache의 tag field의 값과 비교하기 위해서 사용합니다. (상위 비트)
- cache index : block을 선택합니다. 즉 하위 비트를 저장하고 있습니다.
- Byte offset : 하나의 word는 4개의 byte로 이루어져 있으므로, word 안에 몇 번째 byte 인지 명시합니다.
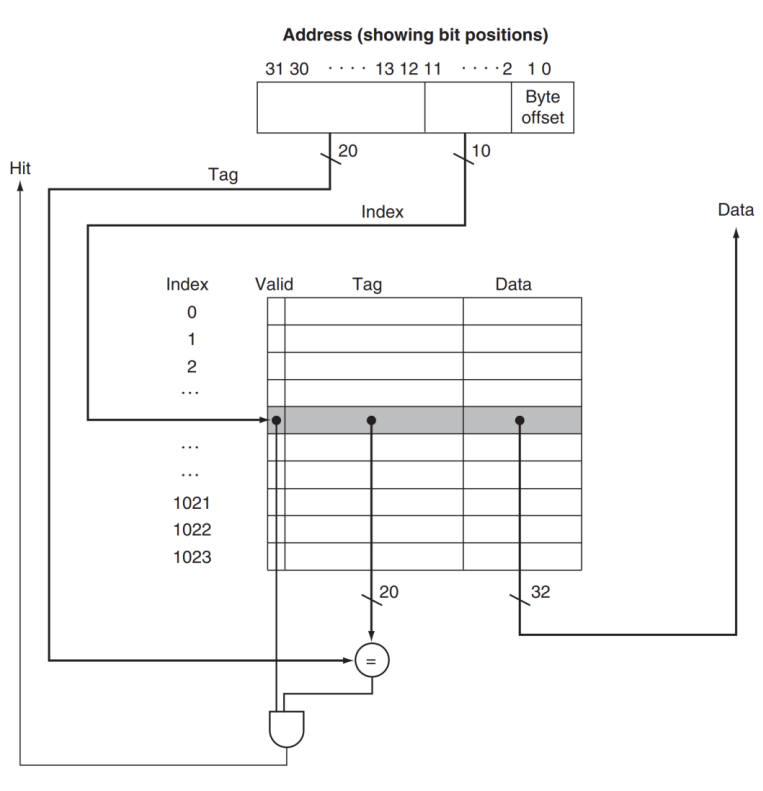
우선 cache index를 이용하여 index 위치로 이동합니다.
이후 cache의 tag field와 reference address의 tag field가 같고, valid가 1이라면 hit이므로,
Byte offset에 대한 Data가 반환됩니다.
이때 Block size는 4 byte로 가정합니다.
(Block은 Valid, Tag를 제외한 Data를 위한 공간임)
따라서 cache index가 10 bit이므로, Cache size는 1024 * 4 byte = 4KB입니다.
(10 bit는
Cache Size와 reference address의 field에 대한 공식은 다음과 같습니다.
32-bit address를 사용하고,
cache가
따라서 cache index는
- Tab field size : 32 - (n + m + 2)
- Total bits of cache =
- the number of bits =
- block 개수 * (block size + tag size + valid field size)
따라서 16 byte인 block 64개로 구성된 cache의 reference address를 봅시다.
우선 block이 64개이므로, cache index bit는 6개입니다.
또한 block size가 16 byte이므로 4개의 bit로 byte offset을 표시할 수 있습니다.

1200번지는 cache의 어느 위치에 mapping 되는지 알아봅시다.
block의 size가 16 byte이므로, 1200 번지는 memory의 75번 block에 해당됩니다.
75 % 64를 하면 11이 나오므로, cache의 11번 block에 위치함을 알 수 있습니다.
긴 글 읽어주셔서 감사합니다.
다음에는 Cache의 Miss를 Handling 하는 방법에 대해 알아보겠습니다.
2022.11.23 - [Computer Science/컴퓨터 구조] - [컴퓨터 구조] Handling Cache Miss
[컴퓨터 구조] Handling Cache Miss
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.11.23 - [Computer Science/컴퓨터 구조] - [컴퓨터 구조] Direct Mapping [컴퓨터 구조] Direct Mapping 앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.11.22 - [Compute
hi-guten-tag.tistory.com
감사합니다.
지적 환영합니다.
'Computer Science > 컴퓨터 구조' 카테고리의 다른 글
| [컴퓨터 구조] Associative Mapping, Cache (0) | 2022.12.04 |
|---|---|
| [컴퓨터 구조] Handling Cache Miss & Write (2) | 2022.11.23 |
| [컴퓨터 구조] The Basic of Cache (0) | 2022.11.22 |
| [컴퓨터 구조] Memory Technologies (0) | 2022.11.22 |
| [컴퓨터 구조] Introduction to the Memory Hierarchy (0) | 2022.11.22 |