앞의 글을 읽으시면 이해에 도움이 됩니다.
2022.04.08 - [Computer Science/머신러닝] - [머신러닝 - 이론] 머신러닝의 기초 (Fundamental of Machine Learning)
[머신러닝 - 이론] 머신러닝의 기초 (Fundamental of Machine Learning)
1. 머신러닝 기초 머신러닝에서 데이터는 중요합니다. 차가 가기 위해 연료가 필요하듯 머신러닝에는 데이터가 필수적입니다. 데이터가 없으면 머신러닝을 적용할 수가 없습니다. 아무것도 가
hi-guten-tag.tistory.com
1. Dimensionality Reduction (차원 축소)란?
차원 축소는 Unsupervised Learning의 한 종류입니다.
다른 종류는 Clustering, Density Estimation이 있고, 해당 종류는 다른 글에서 다룰 예정입니다.
차원 축소는 원래 특징 공간을 저차원으로 변환하는 일을 뜻합니다.
반대로 특징 공간을 고차원으로 변환하는 작업도 있습니다.

첫 번째 이미지는 데이터를 linear하게 분류하지 못합니다.
그러나 이를 다른 좌표계로 공간 변환을 한다면 linear하게 바꿀 수 있고, 차원 축소를 한다면 더 간단히 분류를 할 수 있습니다.

MNIST 데이터는 28 * 28이므로 총 784 차원을 가지고 있습니다.
하지만 그 중 대부분은 숫자가 없는 빈 공간이라서 이런 픽셀들은 제거해도 많은 정보를 잃지 않습니다.
다른 예시로 ILSVRC 데이터의 경우 224 * 224 = 50176 차원을 가지고 있는데,
이것을 그대로 사용한다면 분류도 쉽지 않을 뿐더러 메모리도 초과될 가능성이 높습니다.
실제로 차원이 높을 수록 데이터는 너무 희소하게 분포되어 있습니다.
따라서 데이터 간의 상관관계가 낮아집니다.
데이터가 희소하게 있기 때문에, 이 공간을 밀도가 높게 채우고 싶겠지만, 차원이 하나씩 늘어날 때마다 필요한 데이터의 양은 기하급수적으로 올라갑니다.
따라서 차원에 맞게 데이터를 증가시키는 것 보다는 차라리 데이터에 맞게 차원을 감소시키는 것이 차원 감소의 목적입니다.
차원 축소의 중요한 두 가지 접근법은 투영(projection)과 매니폴드 학습, PCA등 이 있습니다.
Projection을 먼저 보겠습니다.
2. Projection (투영)
실제로 어지간한 훈련 데이터는 모든 차원에 걸쳐 균일하게 퍼져 있지 않고, MNIST처럼 다른 특성들은 서로 강하게 연관되어 있습니다.
결과적으로 샘플은 고차원 공간 안의 저차원 부분 공간 안에 놓여 있습니다.
그림으로 이를 표현하면 아래와 같습니다.


이때 3차원에 보이는 데이터(좌측)는 모든 훈련 샘플이 거의 평면 형태로 놓여져있습니다.
이것이 고차원 공간에 있는 저차원 부분 공간입니다.
여기서 모든 샘플을 평면에 투영한다면 우측 그림과 같은 데이터셋을 얻습니다.
Projection은 이러한 방법을 기반으로 차원을 축소합니다.
하지만 Projection이 완벽한 것은 아닙니다.
만약 스위스 롤 데이터처럼 공간이 뒤틀려있거나, 변환되어 있으면 Projection의 한계가 드러납니다.


만약 Unrolling을 하지 않고 그대로 데이터를 Projection 한다면 아마 우측과 같은 데이터를 얻게 될 겁니다.
그러므로 우리는 이런 데이터에 대해서도 차원을 축소하는 방법을 알아야 합니다.
2. Manifold Learning (매니폴드 학습)
Manifold(매니폴드)란 의미를 보존하는 공간으로 이해하면 될 것 같습니다.
2D Manifold는 2D 형태로 의미를 보존하고, 이를 3D로 나타내면 위의 스위스 롤 같은 3D 데이터가 나옵니다.
매니폴드 학습은 n차원에 있는 d차원 매니폴드(n > d)를 학습해서 저차원에 나타내는 것을 목표로 합니다.
이때 Manifold assumption(매니폴드 가정)은 대부분 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여 있다는 것을 가정합니다.
경험적으로도 이런 가정은 매우 자주 발견된다고 하네요.
바로 처리해야 할 작업이 저차원의 매니폴드 공간에 표현되면 더 간단해질 것이라는 가정입니다.
하지만 이런 가정은 항상 유효하지는 않습니다.
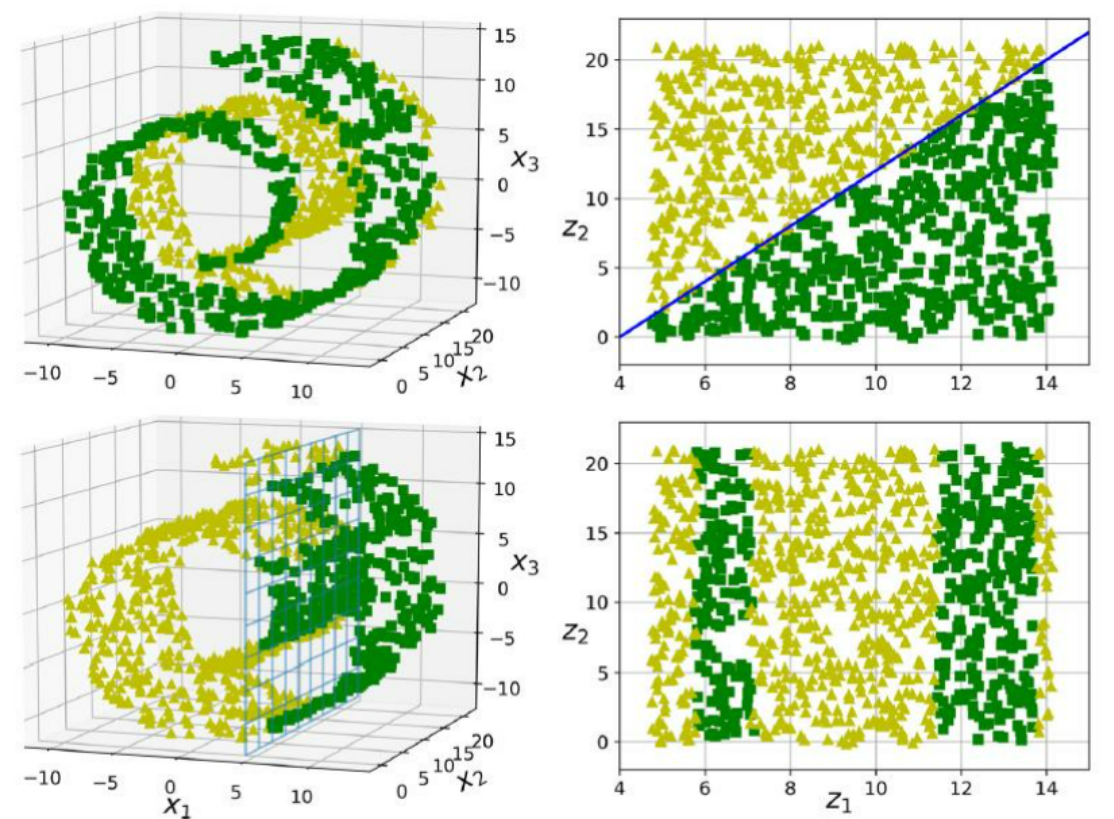
매니폴드를 그대로 2D로 표현했음에도 불구하고 더 복잡해졌습니다.
이는 매니폴드 가정이 항상 더 낫거나 간단한 솔루션이 되는 것이 아니라는 것을 의미합니다.
따라서 다음 글에서는 차원 축소를 위한 대표적인 알고리즘에 대해서 알아보겠습니다.
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] 차원 축소 - PCA, LLE (0) | 2022.10.20 |
|---|---|
| [머신러닝 - 이론] Support Vector Machine (SVM, 서포트 벡터 머신) (0) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Stacking (앙상블 학습 - 스태킹) (2) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Boosting (앙상블 학습 - 부스팅) (0) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Random Forest (앙상블 학습 - 랜덤 포레스트) (0) | 2022.10.19 |