앞의 글을 읽으시면 이해에 도움이 됩니다.
2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Linear Regression (선형 회귀)
[머신러닝 - 이론] Linear Regression (선형 회귀)
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.04.07 - [Computer Science/머신러닝] - [머신러닝 - 이론] 인공지능이란? (What is artificial intelligence?) [머신러닝 - 이론] 인공지능이란? (What is..
hi-guten-tag.tistory.com
2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Polynomial Regression (다항 회귀)
[머신러닝 - 이론] Polynomial Regression (다항 회귀)
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Linear Regression (선형 회귀) [머신러닝 - 이론] Linear Regression (선형 회귀) 앞의 글을 읽..
hi-guten-tag.tistory.com
1. Support Vector Machine (SVM, 서포트 벡터 머신)이란?
SVM은 매우 강력하고 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있을 정도로 다목적 머신러닝 모델입니다.
딥러닝이 나오기 전까지 머신러닝 대회는 모두 SVM일 정도로 강력한 모델이고, 지금도 계속해서 쓰이는 모델이므로 인공지능을 공부하는 사람이라면 필수적으로 알아야 할 모델입니다.
SVM은 분류, 회귀에 따라서 정의가 달라지므로, 먼저 분류에 대해서 살펴보겠습니다.
또한 자세한 수식은 다른 글에서 적도록 하겠습니다.
(해당 글에서는 이해를 위한 수식이 간단히 포함되어 있고, 개념 위주로 설명하도록 하겠습니다.)
2. SVM Classification
SVM 분류의 핵심은 두 클래스 사이의 벡터들의 사이인 마진을 최대화하는 선형 결정 경계를 만드는 Optimal HyperPlane을 찾는 것이 목표입니다.
이때 Support Vector라고 하는 것이 margin을 결정합니다.
Support Vector는 두 클래스를 대표하는 데이터라고 봐도 될 것 같습니다.

이때 SVM이 기존의 linear regression과의 차이점은 바로 마진을 이용한 일반화 능력 향상 기법을 사용한다는 것입니다.
말로 설명하는 것보단 그림이 낫겠습니다.

좌측 그림을 보면 빨간색, 보라색 점은 해당 데이터를 linear separable하게 나누는 모습을 볼 수 있습니다.
그러나 일반화 능력은 떨어지는 모습이 보입니다. 이상한 곳에 새로운 샘플을 넣으면 기존의 결정 경계가 흔들릴 것입니다.
그러나 우측의 SVM을 보면 마진을 이용해 결정 경계를 만들었습니다.
따라서 마진 안에 들어가는 데이터가 아니라면 기존의 결정 경계는 영향을 받지 않습니다.
(= Support Vector 안에 들어가는 데이터가 아니라면)
따라서 SVM이 선형 모델에 비해 좋은 점은 일반화 성능의 향상에 있습니다.
2.1 SVM의 결정 함수
SVM의 결정 함수는
이때 d(x) > 0이라면 양성을, d(x) < 0이라면 음성으로 예측합니다.

2s는 마진(보통 s = 1로 둠)이고, 점선 위에 걸쳐있는 샘플이 바로 support vector입니다.
따라서 SVM의 목표는 마진을 최대화하는 hyperplane의 w를 찾는 것입니다.
그러므로
이때 모든 샘플이 마진 바깥에 올바르게 분류되어 있다면 이를 하드 마진 분류(hard margin classification)이라고 합니다.

하지만 하드 마진 분류에는 두 가지 문제점이 있는데,
첫 번째는 데이터가 선형적으로 구분될 수 있어야 제대로 작동하며,
이상치에 민감합니다.
좌측은 하드 마진을 찾을 수가 없고, 우측은 일반화가 잘될 것 같지 않습니다.
해당 문제를 피하기 위해서는 좀 더 유연한 모델이 필요합니다.
2.2 Soft Margin Classification
소프트 마진 분류는 마진을 최대화하는 것과 마진 오류(margin violation) 사이에 적절한 균형을 잡는 것을 목표로 합니다.
이때 마진 오류는 하이퍼 파라미터 C에 의해 결정됩니다.
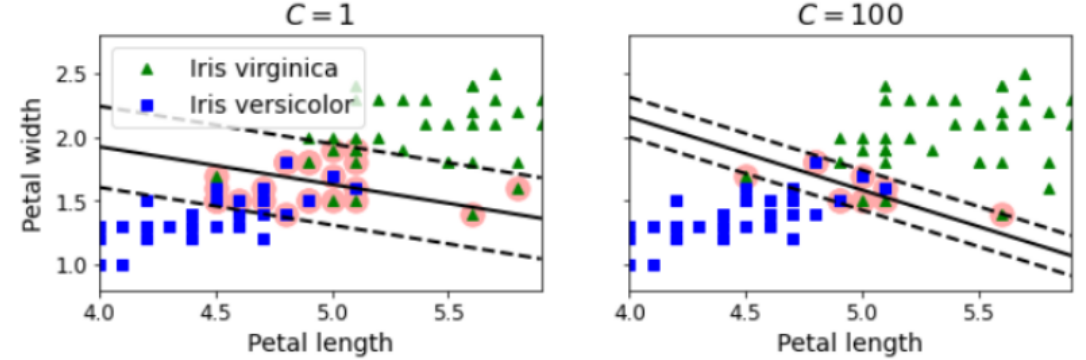
C를 낮게 설정하면 마진 오류를 더 많이 허용합니다.
따라서 일반화 성능이 뛰어납니다.
우측은 마진 오류를 적게 허용하므로, 일반화 성능이 뛰어날 것 같지는 않고, 모델이 OverFitting이 된 모습을 볼 수 있습니다.
C를 낮게 설정한다는 것은 마진 오류를 많이 허용함과 동시에 규제를 강하게 가한다는 뜻(일반화 성능이 뛰어남)으로 보면 될 것 같습니다.
SVM이 OverFitting이 되었다면 C를 감소시켜서 규제를 강하게 가할 수 있습니다.
이제 SVM이 분류 문제를 상대할 때를 봤으니, 회귀 문제에 대해서도 알아봅시다.
3. SVM Regression
SVM Regression은 SVM Classification과는 다르게 제한된 마진 안에 가능한 한 많은 데이터가 들어가도록 학습합니다.
이때 마진의 폭은
따라서 그림은 아래와 같습니다.
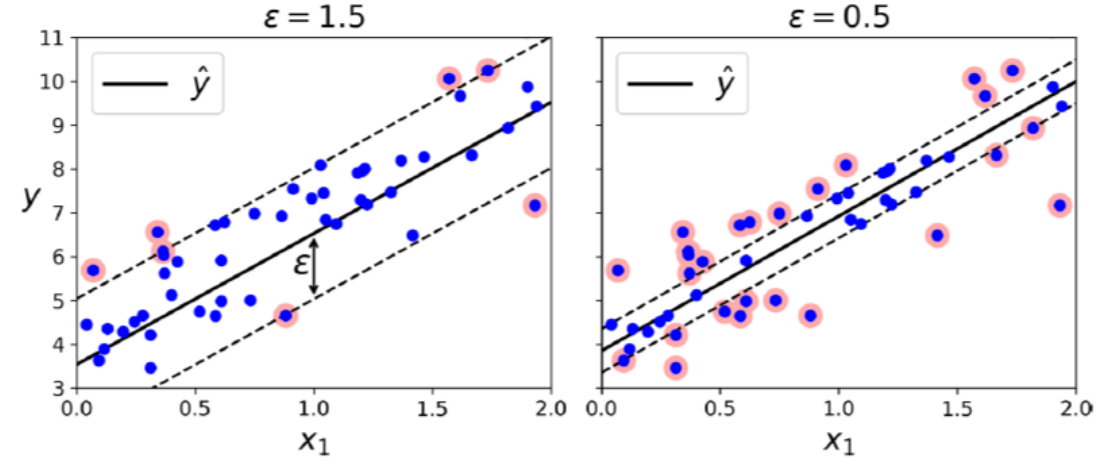
SVM Classification과는 반대로 마진 안에서는 훈련 샘플이 추가되어도 모델의 예측에는 영향이 없습니다.
그래서 이 모델을
이 SVM에도 C를 적용하여 규제를 가할 수 있습니다.
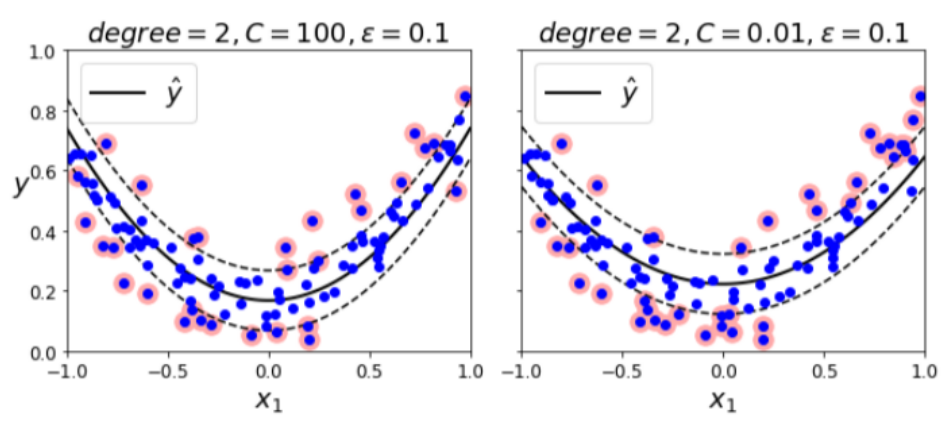
좌측은 OverFitting의 가능성이 커 보입니다.
하지만 우측은 규제를 가하여 노이즈를 최대한 버리고, 일반화된 모습을 볼 수 있습니다.
(사실 뭔 차이인지는 잘 모르겠는데, 확실히 우측이 좌측에 비해서 마진 바깥의 데이터가 더 많은 것 같습니다..)
지금까지는 linear data에 대한 SVM에 대해서 얘기했는데, 다음 글에서는 nonlinear data에 어떻게 SVM을 적용하는지에 대해 설명하겠습니다.
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] 차원 축소 - PCA, LLE (0) | 2022.10.20 |
|---|---|
| [머신러닝 - 이론] Dimensionality Reduction (차원 축소) (2) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Stacking (앙상블 학습 - 스태킹) (2) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Boosting (앙상블 학습 - 부스팅) (0) | 2022.10.19 |
| [머신러닝 - 이론] Ensemble - Random Forest (앙상블 학습 - 랜덤 포레스트) (0) | 2022.10.19 |