[머신러닝 - 이론] Regularization (규제)

---

앞의 글을 읽으시면 이해에 도움이 됩니다.

 

2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Polynomial Regression (다항 회귀)

[머신러닝 - 이론] Polynomial Regression (다항 회귀)

2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] OverFitting, UnderFitting, Cross Validation (과대 적합, 과소 적합, 교차 검증)

[머신러닝 - 이론] OverFitting, UnderFitting, Cross Validation (과대 적합, 과소 적합, 교차 검증)

---

1. Regularization(규제)란?

 

 

앞선 글에서 확인할 수 있듯이 Regularization은 OverFitting을 방지하기 위해 사용됩니다.

 

모델을 규제한다는 것은 모델에게 자유도를 줄인다는 뜻이고, 이는 곧 데이터에 대해 OverFitting을 하기 더 어렵게 만듭니다.

 

다항 회귀 모델을 규제하는 가장 간단한 방법은 다항식의 차수를 감소시키는 것입니다.

 

선형 회귀 모델에서는 보통 모델의 가중치를 제한함으로써 규제를 가합니다.

 

각기 다른 방법으로 가중치를 제한하는 Ridge Regression, Lasso Regression을 살펴보겠습니다.

---

2. Ridge Regression (릿지 회귀)

 

 

릿지 회귀(또는 티호노프 규제, Tikhonov)는 규제가 추가된 선형 회귀 버전입니다.

 

손실함수에 \(a\frac{1}{2}\sum_{i = 1}^{n}\theta^2_i\)를 추가하여, 

\(J(\theta) = MSE(\theta) + a\frac{1}{2}\sum_{i = 1}^{n}\theta^2_i\)를 만듭니다.

(\(\theta_0\)은 편향이므로 포함하지 않음)

 

파라미터들을 제곱해서 더함으로써, 어느 파라미터가 과도하게 커지는 것을 방지합니다.

 

하지만 규제 항보다 MSE가 더 중요하기 때문에 앞에 a(하이퍼 파라미터)를 곱하여 조절합니다.

 

모델의 훈련이 끝나면 모델의 성능을 규제가 없는 성능 지표로 평가합니다.

 

아무튼 a가 0이라면 릿지 회귀는 선형 회귀와 같아집니다.

하지만 a가 아주 크면 결국 모든 데이터는 평균을 지나는 수평선이 됩니다.

좌측은 릿지 모델, 우측은 다항 회귀에 릿지 규제를 적용한 것

우측 이미지에서 a가 1에 가까울수록 곡선이 완만하고, 0에 가까울수록 OverFiting이 됨을 알 수 있습니다.

 

w를 특성의 가중치 벡터라고 정의하면, 규제항은 \(\frac{1}{2}(\left\| w \right\|_2)^2\)와 같습니다.

 

이때 \(\left\| \dots \right\|_2\)는 l2 norm이라고 합니다.

 

결론적으로 Ridge Regression은 어느 한 가중치 벡터(파라미터)를 크게 하지 않으면서, 전체적으로 잘 흩어지게 하는 효과가 있습니다.

---

3. Lasso Regression

 

 

라쏘 회귀는 Ridge처럼 l2 norm을 사용하지 않고, l1 norm을 사용합니다.

 

따라서 손실 함수는 \(J(\theta) = MSE(\theta) + a\sum_{i = 1}^{n}\left| \theta_i \right|\)이 됩니다.

 

좌측은 리쏘 모델, 우측은 다항 회귀에 라쏘 규제를 적용한 것

비슷한 a 값이라도 Lasso 규제가 Ridge 규제에 비해 더 강하게 규제하는 모습을 볼 수 있습니다.

 

왜 그럴까요?

 

라쏘 회귀의 중요한 특징은 덜 중요한 특징을 제거하려 한다는 점입니다.

 

우측 그림에서 a = 1e - 7일 떄는 거의 3차 방정식과 비슷한데, 이는 차수가 높은 다항 특성의 가중치를 0으로 만들었다는 뜻입니다.

 

즉 라쏘 회귀는 자동으로 특성을 선택하여 희소 모델(sparse model)을 만듭니다.

 

 

통상적으로 라쏘보다는 릿지가 더 좋은 성능을 낸다고 알려져 있습니다.

---

4. Early Stopping

 

 

마지막으로 또 다른 규제는 바로 Early Stopping(조기 종료)입니다.

 

경사 하강법과 같이 반복적인 학습 알고리즘을 규제하는 또 다른 방식은 검증 오차가 최솟값에 도달하면 훈련을 중단하는 것입니다.

 

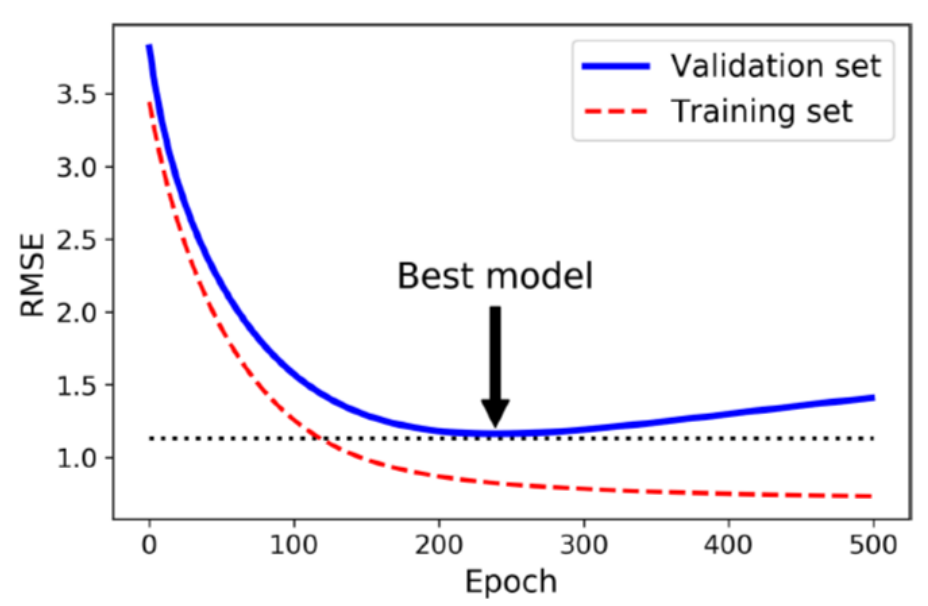
해당 모델을 보면 epochs가 진행됨에 따라 오차가 줄어들다가, 다시 상승합니다.

 

이는 모델이 과대 적합되기 시작했다는 것을 의미합니다.

 

따라서 조기 종료는 검증 오차가 최소에 도달하는 즉시 훈련을 멈춥니다.

(혹은 조금 더 훈련을 하다가, 오차의 상승이 확인되면 최솟값에 해당하는 파라미터를 복구합니다.)

 

감사합니다.

 

지적 환영합니다.