앞의 글을 읽으시면 이해에 도움이 됩니다.
2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Polynomial Regression (다항 회귀)
[머신러닝 - 이론] Polynomial Regression (다항 회귀)
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Linear Regression (선형 회귀) [머신러닝 - 이론] Linear Regression (선형 회귀) 앞의 글을 읽으시면 이해
hi-guten-tag.tistory.com
1. OverFitting, UnderFitting이란?
OverFitting은 과잉 적합, 과대 적합으로 불리며, 모델이 훈련 데이터에 너무 과도하게 맞춰져 있는 것을 의미합니다.
그렇기 때문에 새로운 데이터를 예측해야 할 때, 기존의 훈련 데이터에 과도하게 맞춰져 있으므로, 새로운 데이터를 잘 예측하지 못합니다.
앞선 글인 다항 회귀 글에서 degree가 2보다 큰 상황을 생각하면 쉽게 알 수 있습니다.

degree = 300일 때는 모델이 심각하게 훈련 데이터에 집중되어 있는 모습을 볼 수 있습니다.
UnderFitting은 모델이 훈련 데이터를 너무 과소하게 적합되어 있음을 의미합니다.
이 또한 마찬가지로 새로운 데이터를 예측할 때, 새로운 데이터를 잘 예측하지 못합니다.
이 말은 곧 Generalization(일반화 성능)이 떨어진다는 것과 마찬가지며, 해당 모델이 아무리 높은 성능을 낼 수 있더라도, 이 일반화 성능이 떨어진다면 신뢰하기 어렵습니다.
이 경우에는 degree = 2 일 때 가장 일반화가 잘 되어 있는 모습입니다.
데이터를 볼 수 있는 경우라면 우리가 추정해서 degree를 맞추는 것이 옳은 방법이겠지만,
현실은 그렇게 녹록지 않습니다.
데이터를 볼 수 없는 경우도 수두룩하고, 2차원 공간 상에서 볼 수 있을지도 의문입니다.
그렇기 때문에 일반적으로 어떤 함수로 데이터가 생성되었는지 알 수 없습니다.
그렇다면 얼마나 복잡한 모델을 사용할지 어떻게 알 수 있을까요?
또, 모델이 overfitting, underfitting이 되었는지 어떻게 알 수 있을까요?
통상적으로는 교차 검증을 사용해서 알아낼 수 있습니다.
2. Cross Validation (교차 검증)이란?
교차 검증은 훈련 데이터를 여러 개로 나누어서 학습과 검증을 하는 방식입니다.
사실 overfitting, underfitting을 위해서만 사용하는 것은 아니고, 모델의 일반화를 위해서도 종종 사용하는 기법입니다.

이처럼 데이터를 여러 개로 나눠서 학습과 검증을 따로 합니다.
이렇게 하는 이유가 무엇일까요?
단순히 훈련 데이터와 테스트 데이터를 나누어서 학습을 한다면,
우리는 당연히 테스트 데이터에 더 잘 맞는 모델을 선택하게 될 것입니다.
만약에 테스트 데이터가 우연히 a Label에 편향되어 있고, 해당 테스트 데이터에 잘 맞는 모델을 선택한다면,
그 모델은 당연히 a에 대해 편향된 선택을 하게 됩니다.
그렇기 때문에 테스트 데이터에 대한 신뢰성이 현저히 떨어지게 됩니다.
한 번도 보지 못한 데이터에 대한 정확도가 결국 모델의 신뢰성(일반화 성능)이 됩니다.
그렇기 때문에 우리는 교차 검증을 이용하여 모델의 일반화 성능을 볼 수 있습니다.
위의 이미지를 보면 5개로 나눠서 평가를 하는 모습을 볼 수 있습니다.
이렇게 하는 이유는 우연히 어느 한 검증 데이터가 a Label에 편향되어 있더라도,
다른 검증 데이터가 있기 때문에 이를 보완할 수 있습니다.
따라서 5개의 검증 데이터에 대한 정확도를 평균을 낸 뒤, 가장 좋은 성능을 내는 모델을 선택하면 됩니다.
그리고 해당 모델에 대해서 최종적으로 테스트 데이터에 대한 정확도를 냅니다.
(보통 논문에서 결과를 내기 직전에 한 번 한다고 알고 있음)
이렇게 하면 테스트 데이터는 새롭게 보는 데이터가 되는 것이고, 이에 따른 정확도는 신뢰성이 있겠죠?
3. 교차 검증으로 판단하는 법
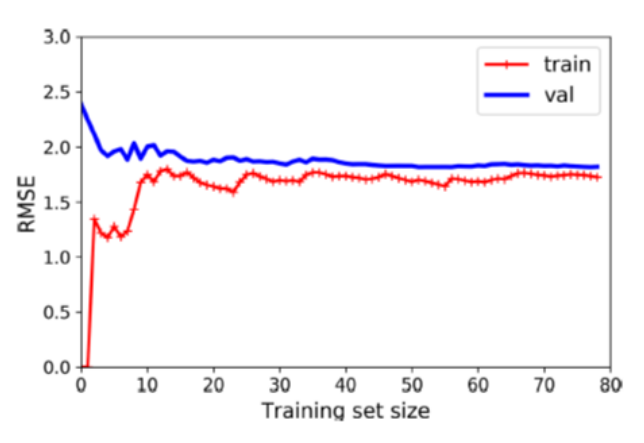
해당 그림을 보면 꽤 높은 지점의 오차에서 검증 데이터와 훈련 데이터가 평행함을 알 수 있습니다.
데이터가 추가되더라도 오차는 낮아지지 않고 그대로입니다.
이는 전형적인 UnderFitting일 때의 그래프이며,
두 곡선이 수평한 구간을 만들고, 꽤 높은 오차에서 매우 가까이 근접해 있습니다.
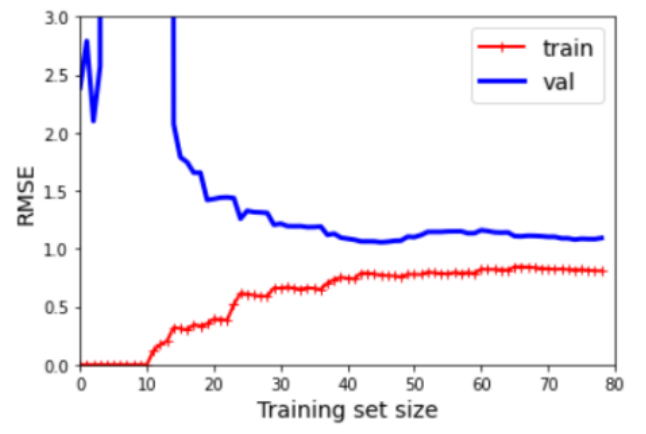
반대로 해당 그림은 꽤 낮은 오차를 가지고 있습니다.
훈련 데이터가 커짐에 따라 오차도 계속 작아지는 모습을 볼 수 있습니다.
다만 훈련 데이터와 검증 데이터 사이에 공간이 있습니다.
이는 모델 성능이 검증 데이터에서 훨씬 낫다는 의미이고, 이는 과대 적합 모델의 특징입니다.
다만 이는 더 많은 훈련 데이터를 사용하면 두 곡선이 점점 더 가까워질 겁니다.
4. 해결법
UnderFitting은 훈련 데이터를 추가해도 효과가 없습니다.
더 복잡한 모델을 사용하던가, 더 나은 특성을 사용해야 합니다.
그와 반대로 OverFitting은 훈련 데이터를 추가하면 해결할 수 있습니다.

과거의 제가 잘 정리해놓았네요 ㅎㅎ
UnderFitting은 단순하게 해결할 수 있지만, OverFitting은 단순히 해결할 수 있는 문제가 아닙니다.
따라서 다음 글에서는 OverFitting을 해결 할 수 있는 Regularization(규제)에 대해서 알아보겠습니다.
2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Regularization (규제)
[머신러닝 - 이론] Regularization (규제)
앞의 글을 읽으시면 이해에 도움이 됩니다. 2022.10.18 - [Computer Science/머신러닝] - [머신러닝 - 이론] Polynomial Regression (다항 회귀) [머신러닝 - 이론] Polynomial Regression (다항 회귀) 앞의 글을 읽으시면
hi-guten-tag.tistory.com
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - 이론] Logistic Regression (로지스틱 회귀) (0) | 2022.10.18 |
|---|---|
| [머신러닝 - 이론] Regularization (규제) (0) | 2022.10.18 |
| [머신러닝 - 이론] Polynomial Regression (다항 회귀) (0) | 2022.10.18 |
| [머신러닝 - 이론] Linear Regression (선형 회귀) (0) | 2022.10.18 |
| [머신러닝 - Python] SIgmoid 계층 구현 (Sigmoid Class Implementation) (1) | 2022.08.20 |