인공지능을 공부하면서 가장 어려웠다고 생각하는 부분입니다.
이해하는 과정이 너무 어려웠고, 구글에 검색해도 죄다 중간 과정은 건너뛰고 결론만 써놓았더라고요..
아무튼 이해하는데 쉽지 않았고, 이 글도 쓸까 말까 고민했습니다.. 너무 양도 많고 어려워서...
해당 글에서는 온갖 수식과 그림이 난무할 테니 집중해서 읽어주시면 아마 오차 역전파를 이해하는데 큰 도움이 되리라 생각합니다.
0. 시작하기에 앞서
오차 역전파를 설명하는 대표적인 두 가지 방법이 있습니다.
수식을 전개해서 설명하는 방법이 있고, 그림을 그려가며 역전파를 이해하는 방법이 있습니다.
상대적으로 그림을 그려가며 이해하는 방식이 쉽지만, 보다 정확한 이해를 위해서는 결국 수식을 통해 증명해야 합니다.
해당 글에서는 둘 다 섞어서 설명할 계획입니다.
처음에는 간단한 수식을 통하여 시작하지만, 끝에는 수식과 그림을 모두 섞어서 설명할 예정입니다.
(수식은 모바일 환경에서는 보이지 않고, pc 환경에서만 보입니다.)
또한 다음 글에서는 계단 함수, 시그모이드 함수, 행렬 등에 대한 오차 역전파에 대하여 얘기할 겁니다.
1. 오차 역전파란?
신경망을 학습하는 방법입니다.
수치 미분과 마찬가지로 해당 가중치가 얼마나 오차에 영향을 끼치는지 알게 해 주며,
쉽게 말해서 손실 함수 위에서의 가중치의 기울기를 알게 해주는 방법입니다.
(기울기에 대한 손실 함수의 미분)
어떤 가중치 w가 오차 L 위에서의 기울기는 \(\frac{\partial L}{\partial w}\)입니다.
앞선 수치 미분에서는 L을 w에 대하여 수치 미분하여 기울기를 알아냈지만, 오차 역전파에서는 연쇄 법칙을 사용하여 알아냅니다.
학습은 \(w \leftarrow w - \eta * \frac{\partial L}{\partial w}\)라는 수식을 통해 학습됩니다.
이때 \(\leftarrow\)는 업데이트가 된다는 뜻이며, \(\eta\)는 학습률(learning rate)입니다.
학습률은 내가 설정하는 하이퍼 파라미터이므로, 중요한 건 \(\frac{\partial L}{\partial w}\)를 구하는 방식입니다.
혹시 선형 대수학 하셨나요?
선형 대수학을 공부하셨다면 아마 연쇄 법칙(=chain rule)에 대해서 아실 겁니다.
아무튼 \(\frac{\partial L}{\partial w}\)을 구하기 위해서 우리는 연쇄 법칙을 우선 알아야 합니다.
2. 연쇄 법칙 (chain rule)
연쇄 법칙을 알기 위해서는 우선 합성 함수부터 알아야 합니다.
합성 함수는 여러 함수로 구성된 함수입니다.
예를 들어 \( z = (x + y)^2\) 라는 함수는 두 개의 식으로 구성됩니다.
\(z = t^2\)
\(t = x + y\)
연쇄 법칙은 합성 함수의 미분에 대한 성질이며, 다음과 같이 정의됩니다.
"합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다."
어렵게 보이지만, 실제로는 간단한 성질입니다.
예를 들어 설명하자면,
\(\frac{\partial z}{\partial x}\) (x에 대한 z의 미분)은
\(\frac{\partial z}{\partial t}\) (t에 대한 z의 미분)과 \(\frac{\partial t}{\partial x}\) (x에 대한 t의 미분)의 곱으로 나타낼 수 있다는 뜻입니다.
즉

으로 나타낼 수 있습니다.
이때 \(\partial t\)를 서로 지울 수 있으므로 해당 수식은 성립합니다.
그렇다면 이제 연쇄 법칙을 사용하여 미분 \(\frac{\partial z}{\partial x}\)를 구해봅시다.

그리고 최종적으로 \(\frac{\partial z}{\partial x}\)는 위의 식에서 구한 두 미분을 곱해 계산합니다.

이게 연쇄 법칙의 끝입니다.
이러한 방식을 통해서 오차 역전파가 계산이 되며, 신경망이 학습을 할 수 있습니다.
3. 국소적 계산
우선 국소적 계산을 이해하기 위해서는 다음 내용을 이해해야 합니다.
입력값 \(x\)가 어떤 함수 \(f\)를 통해서 \(y\)로 출력된다고 합시다.
그렇다면 \(f(x) = y\)가 됩니다.

해당 그림처럼 상류에서 \(\frac{\partial L}{\partial y}\)라는 신호가 흘러들어왔습니다.
(지금은 \(\frac{\partial L}{\partial y}\)가 뭔지 몰라도 상관없습니다. 그냥 역으로 신호가 왔다는 것만 알면 됩니다.
해당 함수는 \(x -> f -> y\)가 순방향입니다.)
이때 \(x\)가 \(L\)에 어떻게 영향을 끼치는지를 알고 싶다는 것이 중요합니다.
그러므로 구해야 하는 수식은 \(\frac{\partial L}{\partial x}\)이고,
현재 내가 알고 있는 값은 상류에서 흘러들어온 신호인 \(\frac{\partial L}{\partial y}\)와 \(f(x) = y\)가 전부입니다.
위의 연쇄 법칙에 근거하여 \(\frac{\partial L}{\partial y} = \frac{\partial L}{\partial y} * \frac{\partial y}{\partial x}\)라는 수식을 알 수 있습니다.
\(\frac{\partial L}{\partial x}\)가 알고 싶으니, 내가 알아야 하는 것은 \(\frac{\partial y}{\partial x}\)가 되겠습니다.
나는 \(f(x) = y\)를 알고 있으니, \(f(x)\)에서 \(\frac{\partial y}{\partial x}\)를 구하면 됩니다.
즉 \(f'(x)\)를 구하면 되겠네요.
가령 \(y = f(x) = x^2\)라면 \(\frac{\partial y}{\partial x} = 2x\)가 됩니다.
그리고 이 미분을 상류에서 전달된 값(이 예에서는 \(\frac{\partial L}{\partial y}\))에 곱하여 앞쪽 노드로 전달하는 것입니다.
그러면 \(\frac{\partial L}{\partial y} * 2x(=\frac{\partial y}{\partial x})\) 이므로 이 값은 \(\frac{\partial L}{\partial x}\)가 됩니다.
이해가 되시나요?
이제는 \(\frac{\partial L}{\partial y}\)가 어떤 존재인지 아셨을 거라 믿습니다.
해당 미분은 상류에서 흘러내려온 미분이며, 위의 순서와 똑같이 흘러서 현재의 \(f\)에 도달하게 된 겁니다.
약간 재귀의 개념과 비슷하다고 생각하면 될 것 같습니다.
결론적으로 \(f(x) = y\)가 있을 때, 상류에서 내려오는 신호를 하류로 흘려보내는데,
하류로 흘려보낼 때 \(\frac{\partial y}{\partial x}\)를 곱해주면 되는 일입니다.
그렇다면 하류로 갈 때는 \(\frac{\partial L}{\partial x}\)이 흘러가게 됩니다.
이때 왼쪽에서 오른쪽으로 진행하는 단계를 순전파(forward propagation)이라고 합니다.
그 반대 방향, 미분이 난무하는 단계를 역전파(backward propagation)이라고 합니다.
위의 단계를이해하셨다면, 이제 국소적 계산이 무엇인지 살펴봐야 합니다.
국소적이란 '자신과 직접 관계된 작은 범위'라는 뜻입니다.
국소적 계산은 결국 전체에서 어떤 일이 벌어지든 상관없이 자신과 관계된 정보만을 결과로 출력할 수 있다는 것입니다.
위의 예와 마찬가지로 \(\frac{\partial L}{\partial y}\)가 뭔지도 모르고 어떻게 발생된건지 몰라도,
해당 \(f\)에서는 역전파로 그냥 \(\frac{\partial y}{\partial x}\)를 곱해서 하류로 흘려보낸 것이 계산의 끝입니다.
전체 계산이 아무리 복잡하더라도 각 단계에서 하는 일은 해당 노드의 '국소적 계산'입니다.
국소적 계산은 단순하지만, 그 결과를 전달함으로써 전체를 구성하는 복잡한 계산을 해낼 수 있습니다.
마치 키보드에는 ㄱ,ㄴ,ㄷ 등 하나의 글자만 있지만, 이것들이 모여 하나의 문장이 되는 것처럼 작동합니다.
4. 곱셈 노드와 덧셈 노드에서의 역전파
4.1 덧셈 노드에서의 역전파
여기서는 덧셈 노드의 역전파에 대해서 알아보겠습니다.
\(z = x + y\)가 있다고 할 때,
\(\frac{\partial z}{\partial x} = 1\)
\(\frac{\partial z}{\partial y} = 1\)
이 됩니다.
이를 계산 그래프(계산을 위한 그래프)로 그리면,
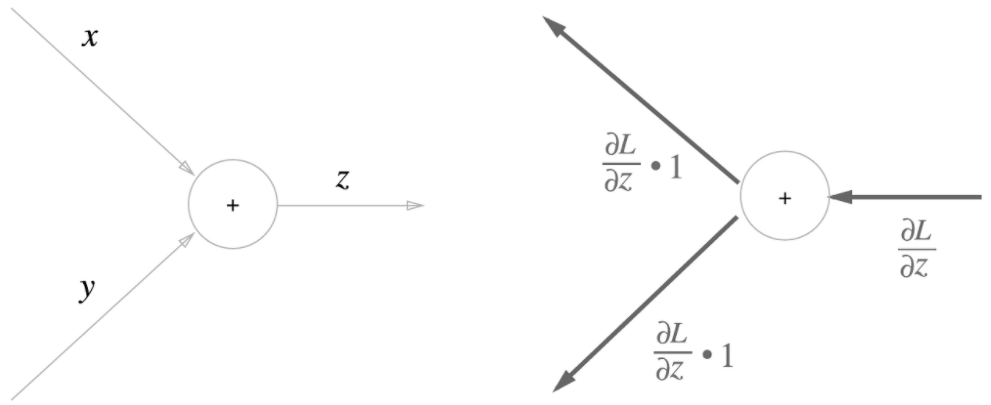
이 됩니다.
상류에서 내려온 신호인 \(\frac{\partial L}{\partial z}\)에 \(\frac{\partial z}{\partial x}\)를 곱함으로써 \(\frac{\partial L}{\partial x}\)을 구했습니다.
물론 덧셈이기 때문에 \(\frac{\partial z}{\partial x} = 1\)입니다.
즉 덧셈 노드는 상류에서 내려온 신호 값을 그대로 하류로 전달시켜 줍니다.
4.2 곱셈 노드에서의 역전파
여기서는 덧셈 노드의 역전파에 대해서 알아보겠습니다.
\(z = x * y\)가 있다고 할 때,
\(\frac{\partial z}{\partial x} = y\)
\(\frac{\partial z}{\partial y} = x\)
이 됩니다.
이를 계산 그래프(계산을 위한 그래프)로 그리면,
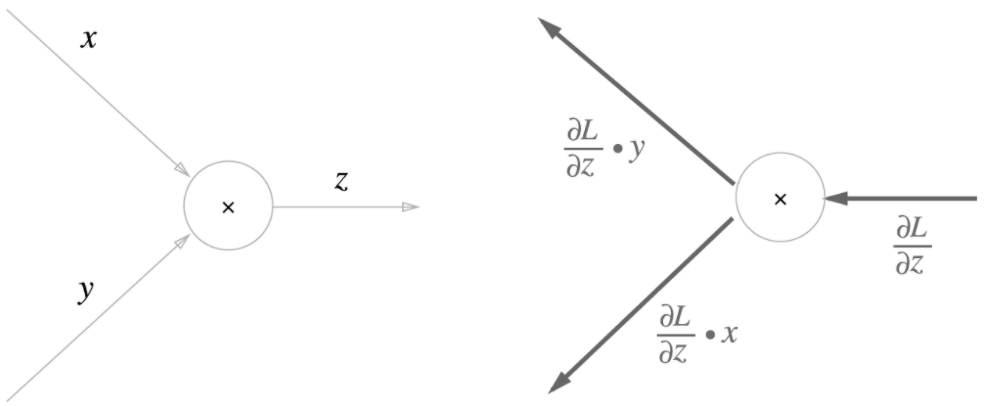
이 됩니다.
상류에서 내려온 신호인 \(\frac{\partial L}{\partial z}\)에 \(\frac{\partial z}{\partial x}\)를 곱함으로써 \(\frac{\partial L}{\partial x}\)을 구했습니다.
이번에는 위와 다르게 \(\frac{\partial z}{\partial x} = y\)입니다.
따라서 곱셈 노드는 상류에서 내려온 신호를 '교차'시켜서 곱한 뒤 다시 하류로 내보낸다고 생각하시면 됩니다.
하지만 본질은 미분입니다.
만약 \(z = x * x\)라면 이 둘을 교차시켜서 상류 신호에 \(x\)를 곱하여 내려 보내는 것이 아닙니다.
이때의 \(\frac{\partial z}{\partial x} = 2x\)임을 명심하셔야 합니다.
5. 연쇄 법칙과 계산 그래프
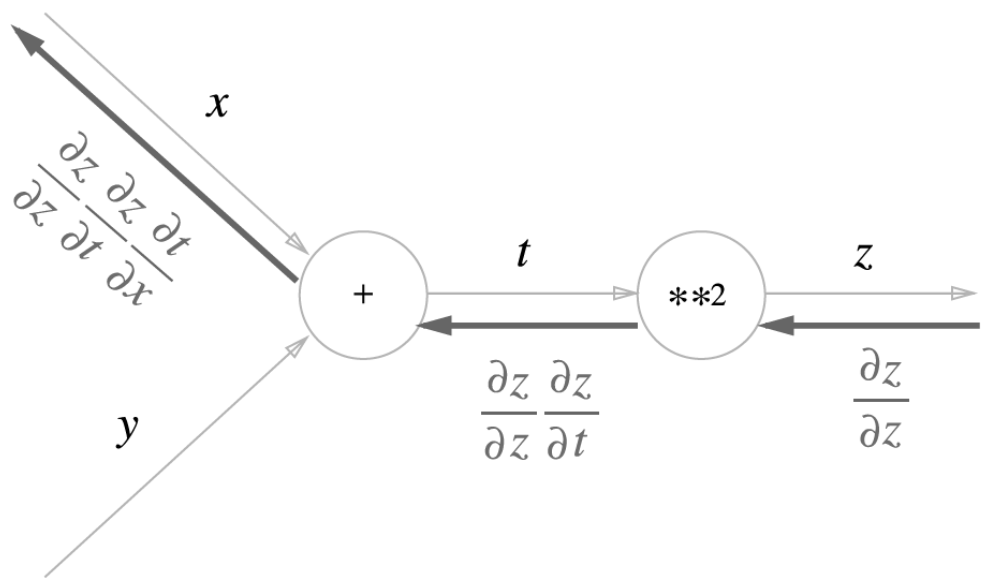
이제는 해당 그래프가 이해가 되시나요?
해당 그래프는 2. 연쇄 법칙에서 설명드렸던 함수 \(z = (x + y)^2\)와 아래의 두 개의 식을 그래프화 한 것입니다.
\(z = t^2\)
\(t = x + y\)
결과 값이 \(z\)이므로 제일 상류에서 내려오는 신호는 \(\frac{\partial z}{\partial z} = 1\)입니다.
위의 계산 그래프를 따라가다 보면 \(x\)에는 \(\frac{\partial z}{\partial z} * \frac{\partial z}{\partial t} * \frac{\partial t}{\partial x}\)가 되므로 결론적으로 \(\frac{\partial z}{\partial x}\)가 남게 됩니다.
즉, x가 z 위에서의 기울기를 알 수 있게 됩니다.
계산을 해보면 \(\frac{\partial z}{\partial t} = 2t\)이고, \(\frac{\partial t}{\partial x} = 1\) 이므로,
아래의 계산 그래프가 나오게 됩니다.
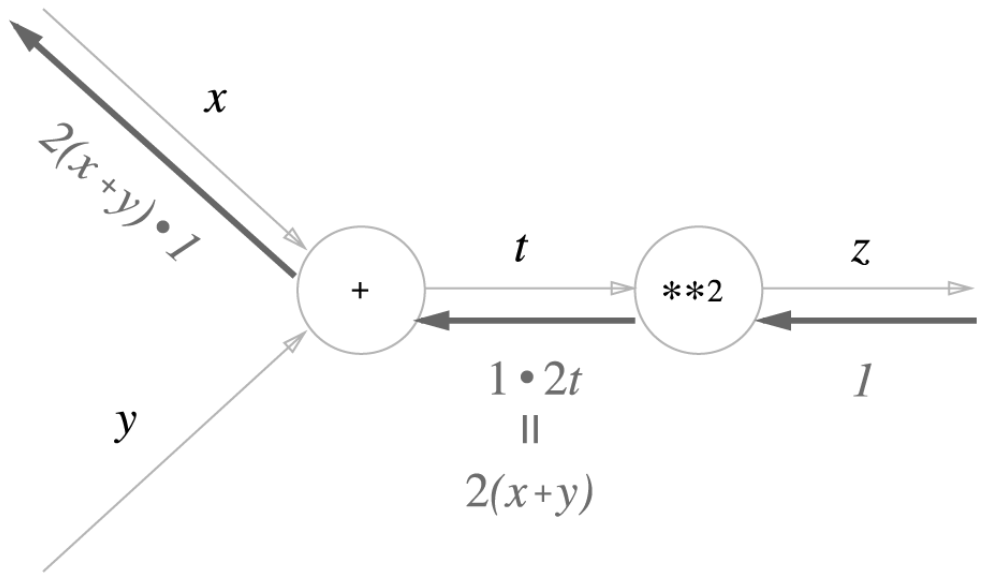
이런 식으로 각 국소적 단계를 통하여 결국 전체 역전파를 계산하게 되고,
이를 바탕으로 학습을 하는 것이 오류 역전파의 핵심입니다.
6. 결론
결론적으로 역전파는 오류를 상류에서 하류로 내려보냄으로써,
각 가중치가 얼마나 오류에 영향을 끼치는지를 알게 해주는 기법입니다.
각 가중치에 대한 오류의 미분을 알기 위해 연쇄 법칙을 사용하며,
연쇄 법칙을 통하여 \(\frac{\partial L}{\partial w}\)를 구함으로써 학습을 합니다.
이때, 수많은 노드와 복잡한 활성화 함수 등이 각 노드에서만의 국소적 계산을 하며,
이러한 값들이 축적되고, 번지면서 결국 한 번의 네트워크 (역)계산으로도 모든 가중치와 편향을 업데이트할 수 있습니다.
곱셈 노드, 덧셈 노드뿐만 아니라 exp 노드, log 노드 등 수많은 노드들이 있지만,
결국 기본 원리는 상류 노드에 해당 노드에서의 미분 값을 찾아서 곱한 뒤, 하류로 흘려보내는 것이 전부입니다.
그러므로 수치 미분보다는 당연히 빠릅니다.
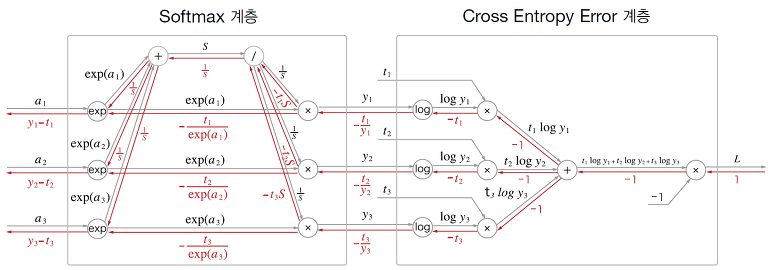
마치 이런 식으로 한 번의 역전파로 모든 가중치와 편향이 업데이트됩니다.
(해당 그림은 추후 설명합니다.)
아무튼 오차 역전파에 대해서 조금이라도 이해하셨기를 빕니다.
만약 조금 더 자세히 알고 싶다면,
해당 글들을 참고해주시기 바랍니다.
위의 글들은 모두 수식으로 이루어져서 그냥 보면 이해하기 힘들지만,
역전파를 조금이나마 이해하셨다면 큰 도움이 될 것 같은 글입니다.
다음 글부터는 활성화 함수에서의 오차 역전파에 대하여 쓰겠습니다.
감사합니다.
지적 환영합니다.
'인공지능 > 머신러닝' 카테고리의 다른 글
| [머신러닝 - Python] ReLU 계층 구현 (ReLU class implementation) (0) | 2022.08.20 |
|---|---|
| [머신러닝 - Python] 덧셈, 곱셈 노드 오차 역전파 구현 (Addition, Multiplication Back Propagation Implementation) (0) | 2022.08.13 |
| [머신러닝 - 이론] 수치 미분 (Numerical Differentiation) (0) | 2022.08.12 |
| [머신러닝 - Python] 2층 신경망 구현 (Two Layer Net Implementation) (0) | 2022.08.06 |
| [머신러닝 - Python] 기울기 구현 (Gradient Implementation) (0) | 2022.08.06 |