1. BST (Binary Search Tree)란?
아마 자료구조 시간에 다 배웠으실 텐데요.
BST는 ordered set (순서 가능한 집합)에 속한 원소(key)로 이루어진 이진 트리이고, 다음의 조건을 만족합니다.
- 각각의 노드는 하나의 unique한 key를 갖고 있다.
- node의 left subtree는 node의 key보다 작거나 같다.
- node의 right subtree는 node의 key보다 크거나 같다.
생각보다 간단하죠?
우리의 목적은 BST에서 검색하는 key와 같은 원소를 찾는 average time을 최소화하는 데 있습니다.
만약에 각 원소가 검색될 확률이 모두 동일하다면, 트리의 높이는 낮을 수록, 그리고 좌우의 높이 차가 덜 클수록 효율적입니다.
하지만 만약에 각 원소가 검색될 확률이 다르다면 어떨까요?
만약에 '김'씨 성과 '우'씨 성을 정렬할 때, 누가 더 많이 검색될까요?
당연히 '김'씨겠죠? 그렇다면 당연히 '김'씨를 상위로 올려놓는 게 당연합니다.
'우'씨는 상대적으로 적게 검색될테니 아래로 놓는 게 더 효율적이죠.
이처럼 각 원소의 key가 검색될 확률은 모두 동일하지 않으므로, 우리는 이것까지 고려해서 최적의 BST를 구현해야 합니다.
이때 원소의 실제 key는 중요하지 않습니다. 중요한 건 확률과 몇 번째에 검색이 되는가가 중요합니다.
즉, p_i가 i노드의 확률이고, c_i가 i노드가 검색될 때까지 비교 횟수라면
T_average = sum(i는 1부터 n까지) c_i * p_i입니다.
예를 들어보겠습니다.
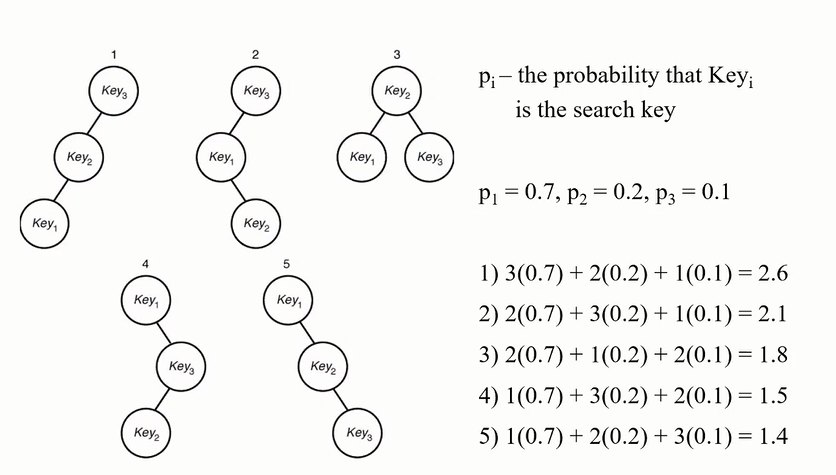
간단하죠?
5번째가 최적이 됨을 알 수 있습니다.
2. 알고리즘
언제나 시작은 brute-force입니다. 모든 경우의 수를 세 본 다음에 비교를 하면 됩니다.
n개의 원소가 있다고 가정해봅시다.
하나의 원소를 제외하고 나머지 원소는 부모 원소의 좌측, 혹은 우측에 위치합니다.
따라서 모든 경우의 수는 2^(n-1)이 되겠네요.
바로 지수 시간 알고리즘이 나와버립니다.
그렇다면 DP를 적용해서 더 좋은 알고리즘으로 풀어봅시다.
만약 K_i부터 K_j까지 최적의 BST로 정렬되어있다고 한다면, 최적 값은 A[i][j]로 표시합니다.
원소가 만약에 하나 있다면 트리에서 원소를 찾는데 비교를 한 번 하므로 A[i][i] = p_i와 같습니다.
이제 DP를 적용하기 위해서 최적의 원칙이 되는지를 알아봅시다.
앞선 그림에서 5번째 그림이 최적의 해가 됩니다.
이때 subtree도 최적인지 한 번 알아봅시다.
A[2][3]을 구해보면,
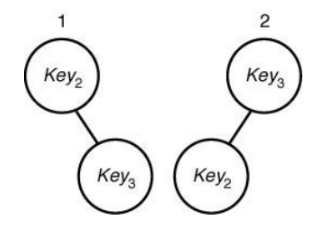
이런 결과가 나옵니다.
단순히 계산해도 key 2가 위에 있는 게 최적 값이네요.
따라서 일반적으로 최적 트리의 하위 트리는 그 하위 트리 안의 원소들에 대해서도 반드시 최적이어야 하므로, 최적의 원칙이 성립합니다.
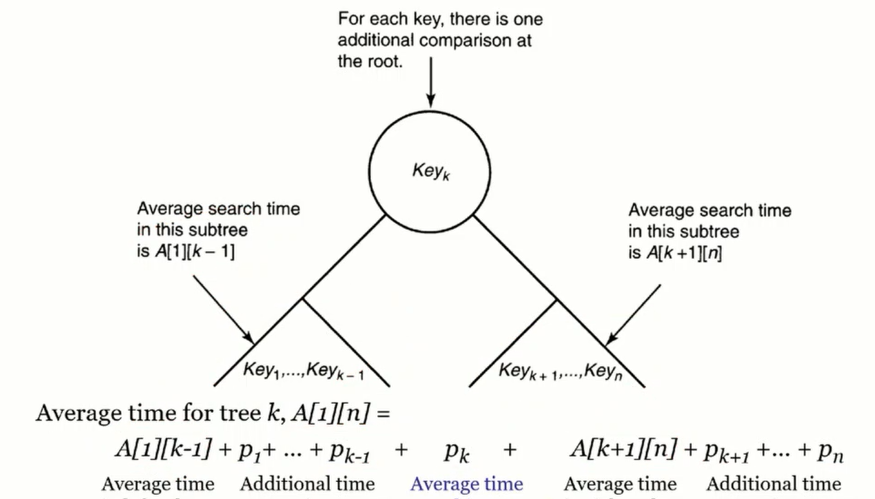
만약 Key k인 노드가 뿌리인 트리가 최적이라면, left subtree가 최적이고, right subtree 또한 최적일 겁니다.
왼쪽 서브 트리의 최적 값은 A[1][k-1]이고, 오른쪽 서브트리의 최적 값은 A[k+1][n]이 됩니다.
이때 Key k를 추가해서 전체 트리를 만든다면, 각 서브 트리에서의 비교 횟수는 기존의 비교 횟수에 추가로 한 번만 더 비교를 하면 됩니다.
따라서 둘을 합친 전체 트리의 최적 값은 (A[1][k-1] + p_1 + ... p_k-1) + p_k + (A[k+1][n] + p_k+1 + ... + p_n)이 됩니다.
이 식을 정리하면 다음과 같습니다.
\(A[1][k-1] + A[k+1][n] + \sum_{m=1}^{n}p_{m}\)
그리고 무수한 k의 경우의 수 중에 하나는 반드시 최적이기 때문에 최적 트리의 평균 검색 시간은 다음과 같습니다.
\(A[1][n] = minimum_{1 \leq k \leq n}(A[1][k-1] + A[k+1][n] + \sum_{m=1}^{n}p_{m})\)
재귀 관계식이 나왔습니다.
이때 k가 0이거나, n이 되면, 좌측 혹은 우측의 서브 트리는 없으므로 A[1][0]과 A[n+1][n]은 0이라고 정의합니다.
따라서 위 식을 일반화 한다면,
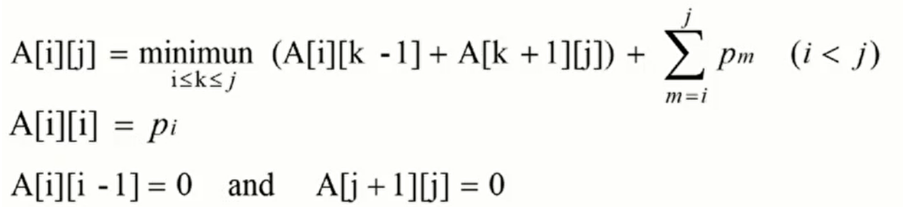
이러한 식이 나오게 됩니다.
이때 배열 R을 만들어서 R[i][j]에는 최적 트리의 루트의 인덱스를 넣게 하면 됩니다.
참고로 트리도 만들어야 하는데, 자세한 건 다음 글의 코드를 참조하시면 될 것 같습니다.
시간 복잡도는 n^3입니다.
코드를 보시면 3중 for loop를 돈다는 걸 아실 수 있습니다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| [알고리즘] 탐욕법이란? (What is the Greedy Approach?) (0) | 2022.04.16 |
|---|---|
| [알고리즘] 동적 계획법 - 최적 이진 탐색 트리 코드 (DP - Optimal BST Code) (0) | 2022.04.15 |
| [알고리즘] 동적 계획법 - 연쇄 행렬 곱셈 코드 (Chained Matrix Multiplication Code) (0) | 2022.04.15 |
| [알고리즘] 동적 계획법 - 연쇄 행렬곱셈 (Chained Matrix Multiplication) (0) | 2022.04.15 |
| [알고리즘] 동적 계획법과 최적화 문제 (Dynamic Programming and Optimization Problem) (0) | 2022.04.15 |