이전 글의 Halting Problem을 기억하시나요?
이처럼 진위 판별을 불가능한 문제가 있고, 진위 판별이 불가능한 문제가 있습니다.
간단하게 진위 판별 문제(결정 문제)로 NP를 제한하면 이론을 전개하기가 쉬워집니다.
우선 결정 문제를 한 번 알아봅시다.
1. Decision Problem
그러기 위해선 우선 지금까지 해온 모든 알고리즘들, Decision Problem과 Optimization Problem에 대해 생각해봐야 합니다.
최적화 문제란 답이 최적해라는 말입니다.
하지만 최적화 문제는 결정 문제로 만들 수 있습니다.
참고로 결정 문제는 yes or no 두 가지 정답만 내놓습니다.
예를 들어서, TSP 문제를 생각해봅시다.
우리는 최소 거리를 구하는 알고리즘을 구현했지만, 만약 특정 거리보다 짧은 거리가 있는지를 판별해야 한다면,
이는 결정 문제가 됩니다.
또한 0-1 KnapSack 문제의 경우, 총 무게가 W가 넘지 않으면서 수익이 최소한 P가 되도록 배낭을 채울 수 있는지를 판별할 수도 있습니다.
위의 문제들에 대해서 결정 문제, 최적화 문제 모두 다항 시간 알고리즘을 찾지 못했습니다.
하지만 어느 하나라도 최적화 문제에 대한 다항 시간 알고리즘을 찾을 수 있다면,
그에 대응하는 결정 문제에 대한 다항 시간 알고리즘도 존재할 것입니다.
예를 들어 TSP에서 최소 거리가 120이라는 사실을 알아냈다면, 이에 대응하는 결정 문제에 대한 답은 아래의 부등 식을 만족하면 "예'가 될 것입니다.
d >= 120
아니라면 "아니오"가 답이 됩니다.
또한 0-1 KnapSack에서 최적 수익이 $230임을 알아냈을 때, 대응하는 결정 문제에서는 P <= $230임을 만족하면 "예", 아니라면 "아니오"가 정답이 될 것입니다.
즉 최적화 문제 -> 결정 문제로 변환 가능이라는 사실을 알 수 있습니다.
최적화 문제를 푸는 다항 시간 알고리즘을 가지고,
그에 대응하는 결정 문제를 푸는 다항 시간 알고리즘을 자동으로 만들어 낼 수 있으므로,
초기에는 결정 문제만 가지고 이론을 전개해봅시다.
먼저 결정 문제를 보고, 이후에는 최적화 문제를 살펴보도록 합시다.
사실 많은 결정 문제에 대해서 그 문제를 푸는 다항 시간 알고리즘을 가지고,
그에 대응하는 최적화 문제를 풀 수있다고 증명되었습니다.
2. P와 NP 집합
이제 본격적으로 P, NP에 대해 알아봅시다.
- P - P는 다항 시간 알고리즘으로 풀 수 있는 모든 "결정 문제의 집합"이다.
- NP - NP는 다항 시간 '비결정적' 알고리즘으로 풀 수 있는 모든 "결정 문제의 집합'이다.
NP는 Nondeterministic Polynomial의 약자입니다.
P의 여집합인지 아닌지는 아직은 모르겠는데, 아닌 것 같습니다.
이는 뒤에서 증명하도록 하겠습니다.
먼저 P를 알아봅시다.
3. 집합 P
어떤 문제가 P에 속할까요?
우선 다항 시간 알고리즘이 있는 결정 문제는 모두 확실히 P에 속합니다.
그렇다면 다항 시간 알고리즘을 찾지 못한 결정 문제도 P에 속할까요?
예를 들어 TSP 결정 문제가 P에 속할까요?
아무도 이 문제를 푸는 다항 시간 알고리즘을 만들지 못했지만, 다항 시간 알고리즘으로 풀 수 없다고 증명한 사람도 없습니다.
따라서 이 문제는 P에 속할 가능성도 있습니다.
그렇다면 어떤 문제가 P에 속하지 않을까요?
일단 확실히 Halting Problem은 P에 속하지 않겠네요. 진위 판별이 불가능, 즉 결정할 수 없으니까요
위의 TSP 결정 문제 같은 경우도 P에 속하는지 안 속하는지 모릅니다.
P에 속하지 않음을 아는 결정 문제는 실제로 거의 없습니다.
P에 속하지 않음을 확실히 아는 문제는 다항 시간 알고리즘이 없다고 증명된 결정 문제밖에 없습니다.
우선 TSP 결정 문제를 확실히 하고 넘어가야 합니다.
누군가가 특정 d보다 작은 경로가 있다고 말했다고 가정하자.
즉, 그 사람은 d에 대해서 주어진 그래프의 총 거리가 d를 넘지 않는 여행 경로가 있다고 말했다.
그러면 그 사람에게 d보다 길지 않은 여행 경로를 실제로 찾아보라고 말할 수 있다.
그러면 우린 verify함수를 아래와 같이 작성할 수 있다.
def verify(S, d):
if S는 여행경로 and S에 속한 가중치의 합 <= d:
return True
else:
return False우선 S가 여행경로라 가정하고 문제를 생각해봅시다.
가중치의 합이 d보다 작다면 true를 넘겨주지만, false를 넘겨준다면 가중치의 합이 d보다 크다는 뜻입니다.
하지만 총 거리가 d 이하의 여행 경로가 없다는 의미는 아닙니다.
총 거리가 d 이하인 다른 여행 경로는 아직 따져보지 않았기 때문입니다.
즉, S를 다른 S로 바꾼다면 해결할 수도 있습니다.
따라서 다른 여행 경로를 검증한다면 해답을 얻을 수도 있습니다.
이 말은 주어진 여행 경로 후보들을 가지고 진위 판별 문제의 해답이 "예' 임을 다항 시간 내에 검증할 수 있다는 뜻을 의미합니다.
4. Polynomial-Time Verifiability (다항 시간 검증 가능성)
NP 집합에 속한 문제들이 지니고 있는 다항 시간 검증 가능성 (Polynomial-Time Verifiability)에 대해 생각해봅시다.
어떤 여행 경로가 주어질 때, 검증 하기 위해서 위해서는 다항 시간이 걸린다고 말했습니다.
하지만 이는 여행 경로를 찾는데 걸리는 시간은 빼고 말한 것입니다.
여행 경로는 이미 다 찾아놨고, 그 후보들 중에서 특정 거리보다 작은 후보가 있는지를 검증하는 것이 다항 시간이라는 뜻입니다.
하지만 검증하는 것이 다항 시간이라는 뜻이 곧 문제를 푸는 것이 다항 시간이라는 것은 아닙니다.
이때 다항 시간 검증 가능성을 좀 더 명확히 설명하기 위하여 비결정 알고리즘(Nonedeterministic Algorithm)을 봐야합니다.
비결정 알고리즘은 두 단계로 이루어져 있습니다.
- (Nondeterministic) Guessing Stage : (비결정) 추측 단계
- 문제의 instance를 가지고 임의의 문자열을 만들어냅니다.
- 이때 문자열은 추측한 해답으로 보면 됩니다.
- 사실 전혀 무의미한 문자열이어도 상관은 없습니다.
- (Deterministic) Verification Stage : (결정) 검증 단계
- 입력은 문제 사례와 추측이고, 궁극적으로 true를 출력하면 멈춘다. (즉 이 사례에 대한 해답이 "예"라고 검증)
- 만약 false라면 출력을 내주면서 멈추거나, 멈추지 않는다.
따라서 위의 verify 함수는 TSP 결정 문제의 검증 단계이며, 결정 알고리즘입니다.
이때 비결정적이 되는 부분은 추측 단계로서 어떻게 해답을 만들어내는지 명시하지 않았으므로 비결정 단계라고 합니다.
아무튼 비결정 알고리즘이 실제로 문제를 풀 순 없지만, 아래의 두 가지 조건을 만족하면 비결정 알고리즘이 결정 문제를 '푼다'라고 말할 수 있습니다.
- 조건 1 : 해답이 "예"가 되는 사례에 대하여 검증 단계의 결과가 "true"가 되는 문자열이 있다.
- 조건 2 : 해답이 "아니오"가 되는 사례에 대하여 검증 단계의 결과가 "true"가 되는 문자열이 없다.
이때 A는 경로지만, 가중치가 d보다 큰 경로, B는 경로가 아닌 것, C는 이상한 문자열, D는 경로이고, 가중치가 d보다 작은 경로라고 가정해봅시다.
이때 verify 함수는 D가 들어온다면 true를 반환합니다.
그렇다면 조건 1을 보면 되겠네요.
D는 경로이고, 가중치가 D보다 작으므로 해답이 "예"가 되고, 검증 결과가 True이므로 조건 1은 만족합니다.
만약 A, B, C를 verify에 넣으면 어떻게 될까요?
아마 verify는 False를 반환할 것입니다.
따라서 조건 2도 만족하게 됩니다.
그러므로 추측 단계에서 단순한 문자열을 생성하고 검증 단계에서 verify 함수를 호출하는
비결정 알고리즘(nondeterministic algorithm)은 TSP 결정 문제를 '푼다' 라고 할 수 있습니다.
그러면 이제 처음으로 돌아가 Polynomial-Time Verifiability를 만족하기 위해서는 비결정 알고리즘의 만족 유무에 따라 알 수 있습니다.
5. NP로 넘어가기 전 이해를 위한 요약
P라는 것은 다항 시간 내에 풀 수 있는 모든 결정 문제의 집합입니다.
우선 다항 시간 알고리즘이 있는 모든 문제는 P에 속하고,
다항 시간 내에 풀 수 없다고 증명한 문제는 P에 속하지 않습니다.
하지만 다항 시간 알고리즘을 만들지 못했고, 다항 시간 내에 풀 수 없다고 증명하지도 못한 문제는 어디에 속할까요?
TSP가 그런 문제의 예시입니다.
이를 위해서 우리는 다항 시간 검증 가능성(ploynomial verifiability)이라는 성질을 이용하고,
이 성질을 좀 더 명확히 하기 위해 비결정 알고리즘(nondeterministic algorithm)의 개념을 도입합니다.
비결정 알고리즘은 두 개의 단계로 나누어서, 각각의 단계가 다항 시간 내에 풀 수 있는지를 알아봅니다.
비결정 알고리즘은 (비결정)추측 단계와 (결정)검증 단계로 이루어져 있으며,
이때 추측 단계는 해답을 내놓는 과정이라 볼 수 있으며, 결정하는 과정이 아니라 추측하는 과정이므로 비결정적입니다.
검증 단계는 추측 단계에서 내놓은 해답이 맞는지를 검증해서 결정하므로 결정적입니다.
다항 시간 내에 "풀 수 있다"는 것은 추측 단계와 검증 단계 둘 다 다항 시간 내에 풀 수 있음을 의미합니다.
하지만 TSP는 추측 단계가 다항 시간인지 아닌지는 모르지만, 검증 단계는 다항 시간임이 확실합니다.
따라서 검증 단계가 다항 시간인 비결정적 알고리즘으로 풀 수 있는 모든 결정 문제는 NP에 속합니다.
즉 검증 단계가 다항 시간이고, 추측 단계가 다항 시간인 문제는 P,
검증 단계가 다항 시간이지만, 추측 단계가 다항 시간인지 아닌지 모르는 문제는 NP에 속합니다.
사실 정확히 따지면 추측 단계는 지수 시간 안에 끝나야 합니다.
만약 추측하는데 무한대가 걸리면 이것은 NP에도 속하지 않는 문제가 된다고 볼 수 있겠습니다.
따라서 P의 여집합은 NP가 아니라, 오히려 P는 NP 안에 속해있는 집합이라 볼 수 있습니다.
이제 NP에 대해서 알아보겠습니다.
6. 집합 NP
우선 다항 시간 비결정 알고리즘(Polynomial-Time Nondeterministic Algorithm)은 검증 단계가 다항 시간 알고리즘인 비결정 알고리즘입니다.
또한 NP는 다항 시간 비결정 알고리즘으로 풀 수 있는 모든 결정 문제의 집합입니다.
예를 들면 소인수 분해가 있겠네요
N = p*q로 분해가 가능하다고 가정합시다.
이때 N을 소인수 분해하는 건 다항 시간이 아닐지라도, p*q가 N임을 검증하는 것은 다항 시간이 맞습니다.
따라서 이러한 문제를 NP라고 할 수 있습니다.
NP는 Nondeterministic Polynomial의 약자임을 다시 한번 생각해야 합니다.
결정 문제가 NP에 속하기 위해서는 다항 시간에 검증을 하는 알고리즘이 반드시 존재해야 합니다.
따라서 TSP는 검증하는 다항 시간 알고리즘이 있으므로, NP에 속합니다.
하지만 검증하는 다항 시간 알고리즘이 있다는 것이, 문제를 푸는 다항 시간 알고리즘이 있다는 뜻은 절대 아니라는 사실을 명심해야 합니다.
그러므로 모든 P는 NP에 속합니다.
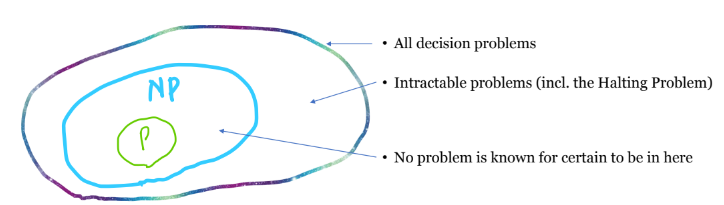
그렇다면 NP에도 속하지 않는 문제가 뭐가 있을까요?
신기하게도 NP에 속하지 않는다고 증명된 결정 문제들은 다루기 힘들다고 증명된, Intractable problem입니다.
이전 글에서 소개했던 Halting Problem이 있습니다.
하지만 위의 집합이 과연 진리일까요?
그것은 아무도 모릅니다.
즉 NP에 속하면서 P에 속하지 않는 문제가 있다고 아직 증명하지 못했기 때문입니다.
P = NP인가? 는 유명한 난제 중 하나입니다.
만약에 P = NP가 사실이라면, 지금까지 알고 있는 대부분의 결정 문제를 푸는 다항 시간 알고리즘이 있다는 얘기입니다.
만약 P != NP임을 증명하려면 NP에 속하면서 P에는 속하지 않는 문제를 찾아야 합니다.
즉 검증 단계가 다항이 아니면서, 추측 단계는 다항인 문제를 찾아야 한다는 뜻입니다.
참 어렵네요
감사합니다.
지적 환영합니다.
'Computer Science > 알고리즘' 카테고리의 다른 글
| [백준 - Python] 1600 - 말이 되고픈 원숭이 (0) | 2023.02.03 |
|---|---|
| [알고리즘 - 이론] NP-Complete, NP-Hard (0) | 2022.06.14 |
| [알고리즘 - 이론] Intractability Algorithm (다루기 힘든 알고리즘) (0) | 2022.06.14 |
| [알고리즘 - Python] BOJ 7450 (2) | 2022.06.12 |
| [알고리즘 - 이론] The Traveling Salesperson Problem : TSP (외판원 문제) (2) | 2022.06.10 |